UStepper robotarm 4: 5 stappe

2024 Outeur: John Day | [email protected]. Laas verander: 2024-01-30 07:25

Dit is die vierde herhaling van my robotarm, wat ek ontwikkel het as 'n toepassing vir ons uStepper stepper -beheerbord. Aangesien die robot 3 stappermotors en 'n servo vir bediening het (in die basiese konfigurasie), is dit nie beperk tot uStepper nie, maar kan dit met enige stepper -bestuurdersbord gebruik word.

Die ontwerp is gebaseer op 'n industriële palletizer -robot - en is relatief eenvoudig. Met dit gesê, het ek ontelbare ure daaraan bestee om die ontwerp te ontwerp en te optimaliseer, beide vir die maklike montering, maar ook om die dele te druk.

Ek het die ontwerp gemaak met die gemak van druk en die eenvoudige montering in gedagte. Nie dat daar geen manier is om hierdie twee parameters te verbeter nie, maar ek dink ek het 'n lang pad gekom. Verder wil ek die industriële robotika tot 'n vlak daal waar stokperdjies dit kan volg deur aan te toon dat dit relatief eenvoudig gemaak kan word - ook die wiskunde om dit te beheer!

Laat gerus 'n opmerking met konstruktiewe terugvoer oor beide die ontwerp, maar veral oor hoe ek dit doen om dit vir almal toeganklik te maak (veral wiskunde).

Stap 1: Onderdele benodig, 3D -druk en montering

Alles wat u moet weet, is in die monteerhandleiding. Daar is 'n gedetailleerde stuklijst met gekoopte en gedrukte onderdele en 'n gedetailleerde monteerinstruksie.

3D -drukwerk word uitgevoer op 'n redelike kwaliteit 3D -drukker (FDM) met 'n laaghoogte van 0,2 mm en 30 % invul. U kan die nuutste weergawe van onderdele en instruksies hier vind:

Stap 2: Kinematika

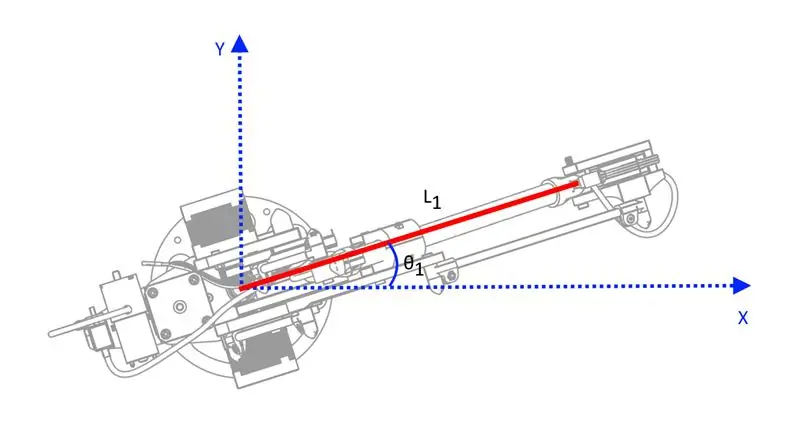
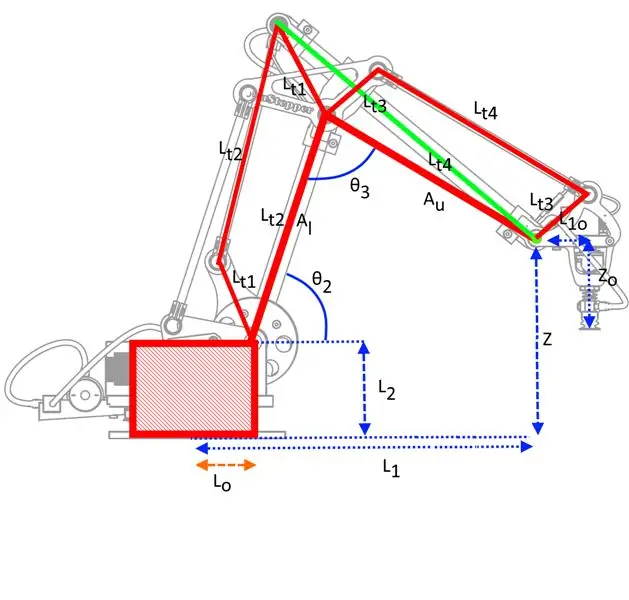
Om die arm op 'n voorsienbare manier te laat rondbeweeg, moet u wiskunde doen: ek het baie plekke gesoek na 'n relatief eenvoudige beskrywing van die kinematika wat verband hou met hierdie tipe robot, maar ek het nie een gevind waarvan ek glo dit was nie 'n vlak waarop die meeste mense dit kon verstaan. Ek het my eie weergawe van die kinematika gedoen, uitsluitlik gebaseer op trigonometrie, en nie die matriks -transformasies wat nogal eng kan lyk as u nog nooit voorheen aan die goed gewerk het nie - dit is egter redelik eenvoudig vir hierdie spesifieke robot, aangesien dit slegs 3 DOF is.

Tog dink ek dat my benadering in die aangehegte dokument relatief maklik verstaanbaar is. Maar kyk of dit vir jou sin maak!

Stap 3: Kodering van die kinematika

Die kinematika kan moeilik wees om te begryp, selfs met die berekeninge wat ek in die vorige gegewens gegee het. Hier is dus eerstens 'n Octave -implementering - Octave is 'n gratis hulpmiddel met baie dieselfde funksies wat in Matlab voorkom.

L1o = 40; Zo = -70; L_2 = 73,0; Au = 188,0; Al = 182,0; Lo = 47,0; UPPERARMLEN = Au; LOWERARMLEN = Al; XOFFSET = Lo; ZOFFSET = L_2; AZOFFSET = Zo; AXOFFSET = L1o; disp ('Kode -implementering') disp ('Invoerhoeke:') rot = deg2rad (30); regs = deg2rad (142,5); links = deg2rad (50); rad2deg (vrot) rad2deg (regs) rad2deg (links) T1 = vrot;#basis T2 = regs; #skouer T3 = links;#elmboog #FW kinematika om XYZ uit hoeke te kry: disp ('Bereken X, Y, Z:') z = ZOFFSET + sin (regs)*LOWERARMLEN - cos (links - (pi/2 - regs))*UPPERARMLEN + AZOFFSET k1 = sin (links - (pi/2 - regs))*UPPERARMLEN + cos (regs)* LOWERARMLEN + XOFFSET + AXOFFSET; x = cos (vrot)*k1 y = sin (vrot)*k1 ## inverse kinematika om hoeke van XYZ te kry: rot = atan2 (y, x); x = x - cos (vrot)*AXOFFSET; y = y - sin (vrot)*AXOFFSET; z = z - AZOFFSET -ZOFFSET; L1 = sqrt (x*x + y*y) - XOFFSET; L2 = sqrt ((L1)*(L1) + (z)*(z)); a = (z)/L2; b = (L2*L2 + LOWERARMLEN*LOWERARMLEN - UPPERARMLEN*UPPERARMLEN)/(2*L2*LOWERARMLEN); c = (LOWERARMLEN*LOWERARMLEN + UPPERARMLEN*UPPERARMLEN - L2*L2)/(2*LOWERARMLEN*UPPERARMLEN); regs = (atan2 (a, sqrt (1-a*a)) + atan2 (sqrt (1-b*b), b)); links = atan2 (sqrt (1-c*c), c); ## output bereken hoeke disp ('Output hoeke:') rot = rad2deg (vrot) regs = rad2deg (regs) links = rad2deg (links)

Met die bogenoemde script het u basies die implementeringskode vir vorentoe en agtertoe kinematika.

Voorwaartse kinematika wat u gebruik om te bereken waar u met 'n gegewe stel motorhoeke sal eindig. Inverse kinematika sal dan (doen die inverse) bereken watter motorhoeke jy nodig het om op die gewenste x, y, z posisie te eindig. Beperkings op motoriese beweging moet dan ingevoeg word, soos bv. rotasie basis kan slegs van 0 tot 359 grade gaan. Op hierdie manier verseker u dat u nie na posisies gaan wat nie haalbaar is nie.

Stap 4: Uitvoering van die ding

Ons is nie heeltemal daar met die implementering van die kinematiese biblioteek nie, sodat ek nog nie kan voorsien nie. Maar ek kan jou 'n video wys van hoe dit verloop. Dit is redelik stabiel en glad as gevolg van die gebruik van laers en riemaandrywing, behalwe die redelike kwaliteit van die aandrywe wat hier die uStepper S -borde is.

Stap 5: Bykomende eindeffektore

Ek het 3 bykomende eindeffektore ontwerp. Die een is eenvoudig 'n horisontale gryper, die ander pas by 'n gewone Europese bier- of koeldrankblik, en laastens is daar 'n vakuumgrypstelsel waarmee u op 'n vakuumbeker, pomp en klep kan sit.

Alles sal hier beskikbaar wees (3D STL-lêers en instruksies):