Simulasie van die sonnestelsel: 4 stappe

2024 Outeur: John Day | [email protected]. Laas verander: 2024-01-30 07:26

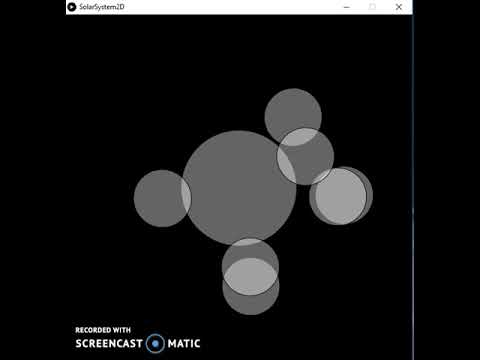
Vir hierdie projek het ek 'n simulasie gemaak van hoe swaartekrag die beweging van planetêre liggame in 'n sonnestelsel beïnvloed. In die video hierbo / word die sonliggaam voorgestel deur die gaasbol, en die planete word lukraak gegenereer.

Die beweging van die planete is gebaseer op die werklike fisika, die Wet van Universele Gravitasie. Hierdie wet definieer die gravitasiekrag wat op 'n massa uitgeoefen word deur 'n ander massa; in hierdie geval die son op al die planete, en die planete op mekaar.

Vir hierdie projek het ek Processing, 'n Java -gebaseerde programmeringsomgewing, gebruik. Ek het ook die verwerkingsvoorbeeldlêer gebruik wat die erns van planete naboots. Al wat u hiervoor benodig, is die verwerkingsagteware en 'n rekenaar.

Stap 1: 2 dimensionele simulasie

Ek het begin kyk na 'n paar video's oor hoe om dit te kodeer wat Dan Shiffman op sy YouTube -kanaal, die Coding Train (deel 1/3), geskep het. Op hierdie stadium het ek gedink dat ek rekursie sou gebruik om die sonnestelsel op te wek, soortgelyk aan hoe Shiffman slegs die fisiese wette doen.

Ek het 'n planeetvoorwerp geskep met 'kinderplanete', wat op hul beurt ook 'kinderplanete' gehad het. Die kode vir die 2D -simulasie was nie klaar nie, omdat ek nie die gravitasiekragte vir elke planeet kon simuleer nie. Ek het van hierdie denkwyse gedraai, in 'n rigting gebaseer op die ingeboude verwerkingsvoorbeeld van gravitasie-aantrekkingskrag. Die probleem was dat ek die gravitasiekrag van al die ander planete op elke planeet moes bereken, maar ek kon nie dink hoe om die inligting van 'n individuele planeet maklik te trek nie. Nadat ek gesien het hoe die verwerkingskursus dit doen, besef ek presies hoe ek dit moet doen met behulp van lusse en skikkings

Stap 2: neem dit in 3 dimensies

Met die voorbeeldkode vir Planetary Attraction wat by die verwerking kom, het ek 'n nuwe program vir 'n 3D -simulasie begin. Die groot verskil is in die Planet -klas, waar ek 'n aantrekkingskragfunksie bygevoeg het, wat die gravitasiekrag tussen twee planete bereken. Dit het my in staat gestel om te simuleer hoe ons sonnestelsels werk, waar die planete nie net deur die son aangetrek word nie, maar ook van elke ander planeet.

Elke planeet het willekeurig gegenereerde eienskappe soos die massa, radius, aanvanklike wentelsnelheid, ens. Die planete is soliede sfere en die son is 'n gaasbol. Boonop draai die kameraposisie om die middel van die venster.

Stap 3: Gebruik regte planete

Nadat ek die raamwerk vir die 3D -simulasie afgeskakel het, het ek Wikipedia gebruik om die werklike planetêre data vir ons sonnestelsel te vind. Ek het 'n verskeidenheid planeetvoorwerpe geskep en die regte data ingevoer. Toe ek dit doen, moes ek al die eienskappe afskaal. Toe ek dit gedoen het, moes ek die werklike waardes geneem het en met 'n faktor vermenigvuldig het om die waardes af te skaal, in plaas daarvan het ek dit in eenhede van die aarde gedoen. Dit is dat ek die verhouding van die aarde se waarde tot die waarde van die ander voorwerpe geneem het, byvoorbeeld dat die son 109 keer meer massa as die aarde het. Dit het egter daartoe gelei dat die grootte van die planete te groot of te klein lyk.

Stap 4: Laaste gedagtes en kommentaar

As ek sou voortgaan om aan hierdie simulasie te werk, sou ek 'n paar dinge verfyn/verbeter:

1. Eerstens sou ek alles eenvormig skaal met dieselfde skaalfaktor. Om die sigbaarheid van die wentelbane te verbeter, sou ek 'n spoor agter elke planeet byvoeg om te sien hoe elke rewolusie vergelyk met die vorige

2. Die kamera is nie interaktief nie, wat beteken dat 'n deel van die wentelbane van die skerm af is, "agter die persoon". Daar is 'n 3D -kamerabiblioteek genaamd Peazy Cam, wat gebruik word in Deel 2 van die Coding Train -video -reeks oor hierdie onderwerp. Met hierdie biblioteek kan die kyker die kamera draai, paneer en inzoom sodat hulle die hele wentelbaan van 'n planeet kan volg.

3. Laastens is die planete tans nie van mekaar te onderskei nie. Ek wil 'velle' by elke planeet en die son voeg, sodat kykers die aarde en so kan herken.