Oplossing van waarheidstabelle: 10 stappe

2024 Outeur: John Day | [email protected]. Laas verander: 2024-01-30 07:24

'N Waarheidstabel is 'n manier om al die uitkomste van 'n probleem te visualiseer. Hierdie instruksieset is gemaak vir mense wat aan die gang kom in diskrete wiskunde. Ons sal vandag oefen met 'n voorbeeldprobleem wat spesifiek is vir hierdie instruksies. U benodig 'n bietjie krappapier en 'n potlood om die tafel te visualiseer. Hierdie probleem behoort ongeveer 5 minute te neem vir mense met voorkennis oor die onderwerp en ongeveer 10 minute vir beginners.

Vir hierdie instruksieset fokus ons op die probleem ~ p Λ q. Ons gebruik dit om 'n paar simbole bekend te stel wat nodig is om waarheidstabelle te interpreteer.

Stap 1: Verstaan die waarheidstabelle

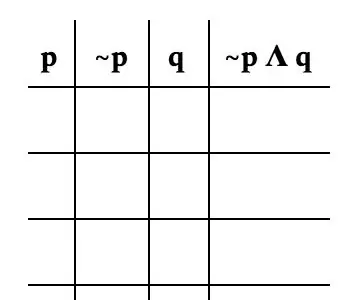
'N Waarheidstabel is 'n manier om al die moontlikhede van 'n probleem te visualiseer. Om waarheidstabelle te ken, is 'n basiese noodsaaklikheid vir diskrete wiskunde. Hier vind ons al die uitkomste vir die eenvoudige vergelyking van ~ p Λ q.

Stap 2: Ken die simbole

Die eerste stap na die waarheidstabel is om die tekens te verstaan. Die '~' in hierdie spesifieke probleem staan vir ontkenning. Die "p" en "q" is beide veranderlikes. Die "Λ" is gelykstaande aan "en". Hierdie vergelyking word gelees as "nie p en q", wat beteken dat die vergelyking waar is as p nie waar is nie en q waar is.

Stap 3: Formateer die tabel

Nou om die werklike tabel te vorm. Dit is belangrik om die probleem met elke veranderlike op te deel. Vir hierdie probleem verdeel ons dit soos volg: p, ~ p, q, en ~ p Λ q. Die beeld is 'n goeie voorbeeld van hoe u tafel moet lyk.

Stap 4: Ken waar en onwaar toe

Aangesien daar slegs twee veranderlikes is, sal daar slegs vier moontlikhede per veranderlike wees. Vir p verdeel ons dit met die helfte van die spasies wat T (vir waar) neem en die ander helfte met F (vir vals).

Stap 5: Ontkenning

Vir ~ p skryf jy die teenoorgestelde teken wat p het sedert ~ p die teenoorgestelde is van p.

Stap 6: Veranderlike "q"

Vir q wissel u tussen T en F om elke moontlike kombinasie te kry. Aangesien die vergelyking slegs op ~ p fokus, kan ons die kolom p ignoreer by die bepaling van die waarheid van die vergelyking. Die "Λ" simbool beteken dat beide ~ p en q waar moet wees vir die vergelyking om waar te wees.

Stap 7: Oplossing vir onwaar in die laaste kolom

Vir die eerste ry, aangesien ~ p F is en q T is, ~ p Λ q is F in die scenario dat ~ p F en q is T. Die enigste scenario waarin die vergelyking T is, is ~ p is T en q is T.

Stap 8: Vind die ware in die laaste kolom

Dit beteken dat die enigste ry wat T is, die derde ry is.

Stap 9: Maak die tabel klaar

Maak seker dat u tafel korrek is. U doen dit deur te kontroleer of u tekens reg is en seker te maak dat die laaste kolom korrek is. Die laaste kolom is die resultaat van al die moontlike permutasies van die veranderlikes.

Stap 10: Klaar

Noudat u weet hoe u 'n basiese waarheidstabel moet doen, moet u aanhou oefen! Hoe meer jy oefen, hoe beter sal jy word om dit te doen.