Oogbal Die voorskrif van u oogbal: 'n BME60B -projek: 9 stappe

2024 Outeur: John Day | [email protected]. Laas verander: 2024-01-30 07:23

Deur: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Vergroting is een van die belangrikste kenmerke van 'n leesbril, wat geklassifiseer word volgens hul voorskrif van dioptrie. Volgens die Michigan Technology University is 'n diopter 'n brandpunt van die lens, gewoonlik gemeet in mm, in die eenheid van meters (Michigan Technology University). Omdat die leesbril konvekse lense het, sal die brandpuntafstand positief wees, wat veroorsaak dat die dioptrie ook positief is (HyperPhysics). Die brandpuntsafstand neem toe namate die afstand tussen die voorwerp verder van die werklike lens af kom, en dit laat die dioptrie afneem omdat dit omgekeerd eweredig is. Daarom sou 'n leesbril met ekstra dioptrië die lens help om in die aansig in te zoem, sodat dit lyk asof die brandpuntsafstand minder is deur die waarde van die dioptrie te verhoog.

Die voorgestelde kode sal gebruik word om die diopter van 'n lens met 'n onbekende voorskrif te voorspel. Twee insette word gebruik om die voorskrif te bereken: 'n foto van die gekontroleerde agtergrond sonder om lense te gebruik, en 'n ander foto van dieselfde agtergrond, maar deur die lens van keuse. Die program sal die vervorming tussen hierdie twee foto's meet. Van daaruit kan ons die diopter van die lens skat en 'n resultaat lewer wat die gebruiker kan sien.

Vir hierdie instruksies benodig u:

• 'N swart-en-wit dambordpatroon gedruk op 'n 11 x 8,5 in vel papier
• 'N Kamera wat die fokus kan sluit
• 'N Statief, of iets soortgelyks om die kamera vas te maak
• Verskeie voorskrifte van leesbrille
• MATLAB

Stap 1: Neem foto's

Om die vergroting van 'n lens te bereken, moet u dit kan vergelyk met die werklike grootte van die voorwerp. Vir hierdie projek vergelyk ons 'n vergrote beeld met 'n kontrolebeeld.

Die eerste stap is dus om twee foto's van dieselfde beeld te neem - die eerste deur net die kamera en die tweede deur die lens van die leesbril wat u wil toets.

U neem 'n foto van 'n 8.5x11in swart en wit dambord met 'n 1in -rooster. Stel u kamera 11in weg van die skaakbord af. Sluit die fokus op die dambord voordat u die foto's neem.

Neem 'n foto van die dam sonder die leesbril. Plaas dan die leesbril voor die kamera sonder om iets te beweeg en neem die tweede foto.

Maak seker dat die posisie van u kamera nie tussen die opnames beweeg nie. Die enigste ding wat tussen die twee foto's moet verander, is die teenwoordigheid van die brillens voor die kamera.

Laai dit na u rekenaar as u klaar is met die foto's.

Stap 2: Laai die beelde in MATLAB

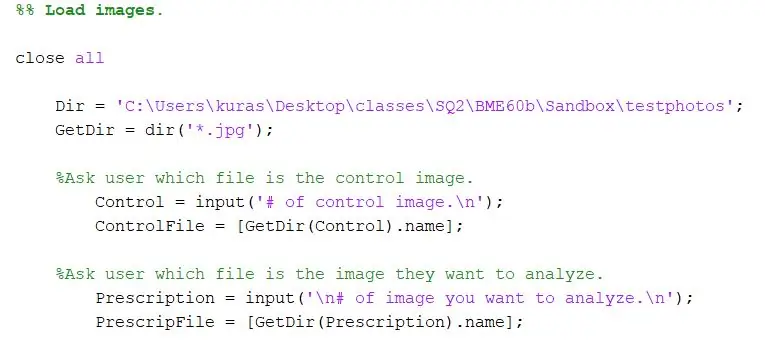
Maak 'n nuwe skrif oop.

Spesifiseer eers die gids waar die foto's gestoor word. Gebruik dan die dir -funksie om-j.webp

Dir = 'C: / Users / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

Vir ons projek wou ons die gebruiker van die program vra vir watter lêers hulle wou vergelyk. Die eerste afdeling vra die gebruiker om die kontrolebeeld te spesifiseer, en die tweede vra die gebruiker om die toetsbeeld te spesifiseer.

• Vra die gebruiker watter lêer die kontrolebeeld is.
• Beheer = invoer ('# van beheerbeeld. / N');
• ControlFile = [GetDir (Control).name]
• Vra die gebruiker watter lêer die prentjie is wat hulle wil ontleed.
• ChooseFile = invoer ('\ n# prentjie wat u wil analiseer. / N');
• PrescripFile = [GetDir (ChooseFile).name];

Stap 3: Beeldanalise

'N Gekleurde beeld in MATLAB is van grootte MxNx3, terwyl 'n grysskaalbeeld MxN is. Dit beteken dat dit vinniger is om 'n grysskaalbeeld te verbeter/te wysig omdat daar minder data is om by te hou. Gebruik rgb2gray om die beeld in grysskaal om te skakel. (Die imrotate -funksie is gebruik omdat ons foto's horisontaal was - hierdie reël kode is in u weergawe al dan nie nodig nie.)

• %verander in grysskaal en draai
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = imrotate (I, 90);

Wys dan die prent. Die subplotfunksie word gebruik sodat die toetsbeeld in latere stappe langs die bedieningspaneel kan wees.

• %vertoon
• Figuur 1);
• subplot (1, 2, 1)
• imshow (I);
• titel (ControlFile);

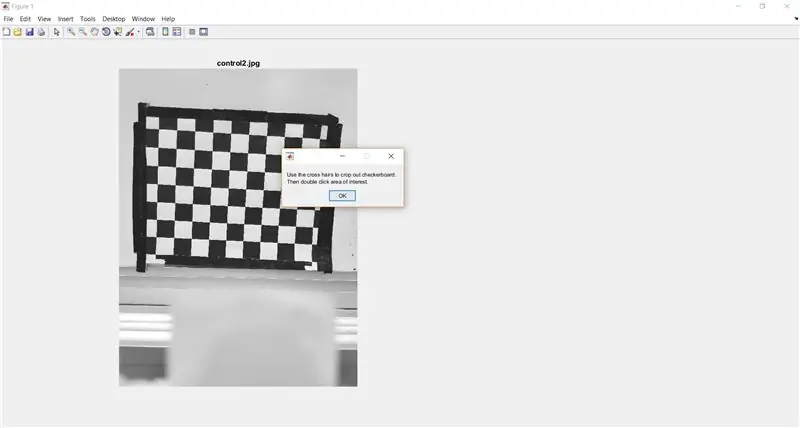
Gebruik imcrop om die gebruiker te vra om die skaakbord uit die volledige prent te sny. Die volgende kode toon ook 'n boodskapkassie om instruksies aan die gebruiker te gee.

• %trek die bord uit vir ontleding
• waitfor (msgbox ({'Gebruik die kruishare om die skaakbord uit te haal.', 'Dubbelklik dan op die area van belang.'}));
• I_crop = imcrop (I);

Gebruik imbinarize om die beeld te binariseer.

I_binary = imbinarize (I_crop);

Stap 4: Bereken die breedte van die wit blokkies op die bord

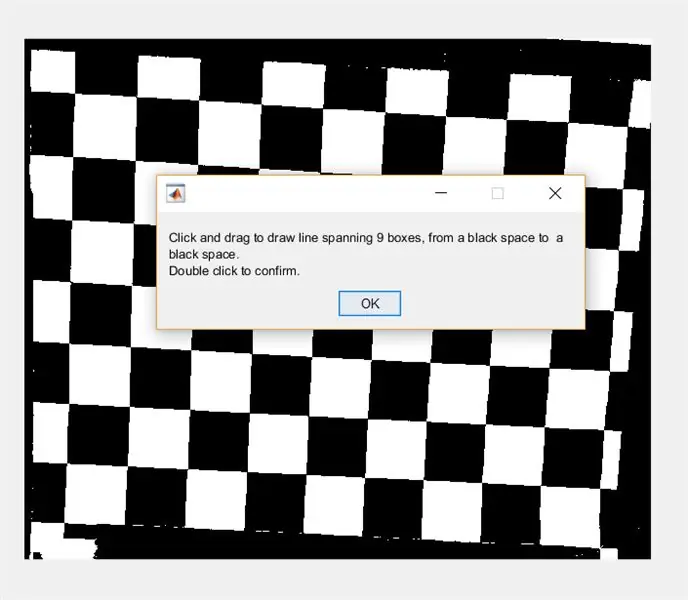
Vra die gebruiker vervolgens om 'n streep oor die prentjie te trek met behulp van imline. Hierdie lyn moet horisontaal oor die skaakbord loop. Dit moet begin en eindig op 'n swart vierkant (dit maak nie saak waar nie)- dit is omdat ons die breedte van die wit vierkante sal meet, nie die swart nie.

• %trek lyn
• Figuur 1)
• subplot (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Klik en sleep om 'n lyn oor 9 bokse te trek, van 'n swart spasie na 'n swart spasie.', 'Dubbelklik om te bevestig.'}));
• reël = imline;
• posisie = wag (reël);
• eindpunte = line.getPosition;

Onttrek die X- en Y -koodinate vir die eindpunte van die getekende lyn.

• X = eindpunte (:, 1)
• Y = eindpunte (:, 2);

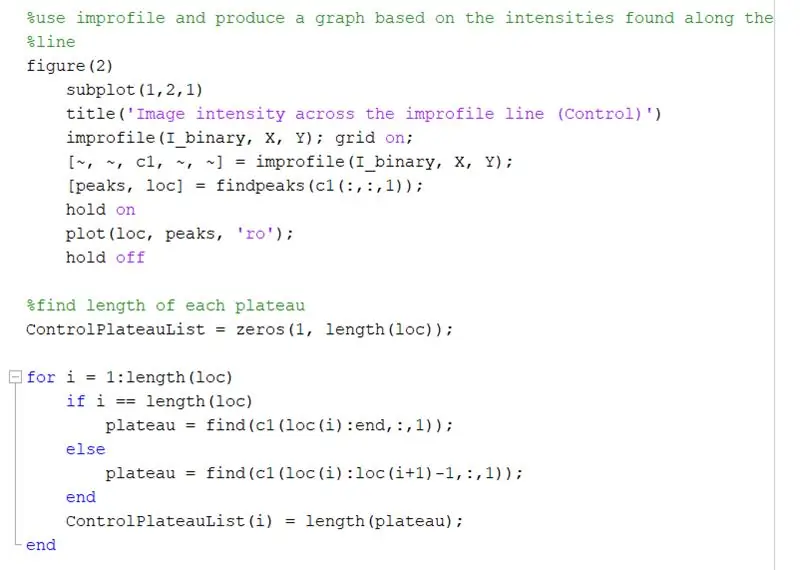
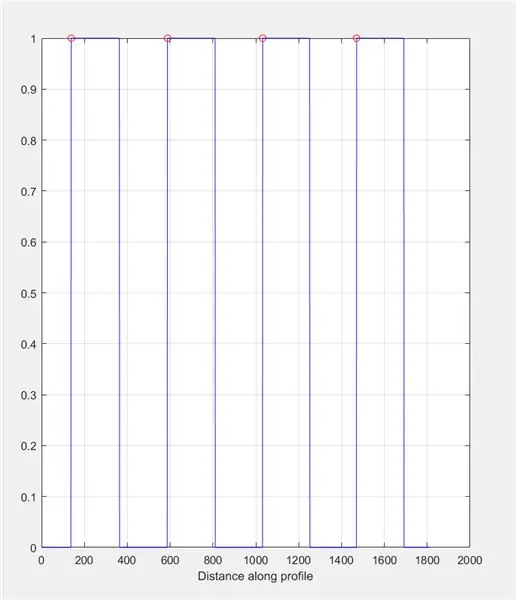
Gebruik onjuiste lêer om 'n grafiek te maak gebaseer op die intensiteite langs die getekende lyn. Dit moet lyk soos 'n vierkantige golf wat wissel van 0 (swart) tot 1 (wit). Bereken ook die pieke en hul ligging.

• figuur (2)
• subplot (1, 2, 1)
• titel ('Beeldintensiteit oor die onfeilbare lyn (beheer)')
• onleesbaar (I_binary, X, Y); rooster op;
• [~, ~, c1, ~, ~] = improfile (I_binary, X, Y);
• [pieke, loc] = vindpieke (c1 (:,:, 1));
• hou vas
• plot (loc, pieke, 'ro');
• hou vas

Bepaal die lengte van elke plato op die grafiek met 'n on -lêer met 'n for -lus. Voer die for -lus uit vir dieselfde hoeveelheid pieke as in die grafiek met die onfeilbare lêer. Om die lengte van elke plato te bereken, gebruik die 'vind' -funksie om al die plekke te vind waar 'n' 1 'in plaas van 'n' 0 'intensiteitswaarde is. Bereken dan die lengte van die skikking om die totale lengte van die plato te kry, wat gelyk moet wees aan die breedte van 'n wit vierkant in pixels. ControlPlateauList = nulle (1, lengte (loc));

vir i = 1: lengte (loc)

as i == lengte (loc)

plato = vind (c1 (loc (i): einde,:, 1));

anders

plato = vind (c1 (loc (i): loc (i+1) -1,:, 1));

einde

ControlPlateauList (i) = lengte (plato);

einde

Stap 5: Herhaal stap 3 en 4 vir die toetsbeeld

*Let wel: as u die onfeilbare lyn op die toetsbeeld trek, moet u dit oor die vierkante trek wat ooreenstem met die lyn wat u op die kontrolebeeld geteken het.

Stap 6: Bereken die vergroting van die lens

Die vergrote metings word bereken deur die gemiddelde van die lengte van die plato, wat in stap 5 bereken is, te deel deur die gemiddelde van die lengte van die beheerplato, wat bereken is in stap 4. Dit word bereken op 1.0884.

vergroting = gemiddelde (plateauList)/gemiddelde (ControlPlateauList);

Stap 7: Vind R-kwadraat en die voorskrif van die gebruiker via interpolasie

Gebruik die kode:

• md1 = fitlm (GivenPrescription, MagArray);
• Rsquared = md1. Rsquared. Oordinaal;

Ons kan die R-kwadraatwaarde van die grafiek GivenPresciption (ons lense se gegewe waardes) teenoor MagArray ('n verskeidenheid van die vergrotingsmetingsverhoudings wat ons vroeër bereken het) vind. Deur 'n hoë genoeg R-kwadraatwaarde te hê, kan afgelei word dat daar 'n sterk genoeg korrelasie is om die gebruik van hierdie metode te regverdig. Vir hierdie spesifieke geval was die R-kwadraatwaarde 0.9912, wat dui op 'n sterk korrelasie en daarom is dit geregverdig om hierdie metode in analise te gebruik.

Gebruik die funksie:

Voorskrif = interp1 (MagArray, GivenPrescription, vergroting, 'lineêr');

Ons kan die ooreenstemmende voorskrifwaarde (op die x-as) van ons vergrotingsverhouding ('n waarde op die y-as) interpoleer en vind wat die gebruiker se voorskrif is.

Dit is belangrik om data te interpoleer om hierdie metode te laat werk, aangesien dit ons toelaat om aannames te maak oor inligting wat ons nie het nie, gebaseer op die inligting wat ons wel het. Alhoewel die beste pasmaatreël tegnies 'n sterker kandidaat vir hierdie aanname sou wees, het die skep van grense om die aantal uitsette te verminder dieselfde effek as wat voorgeskrewe bril in elk geval inkrementele eenvormige waardes het. Dit word in latere stappe verduidelik.

Stap 8: Die voorskrif van die gebruiker op 'n grafiek

Gebruik die volgende kode:

• figuur;
• plot (GivenPrescription, MagArray, '-g')
• hou vas
• plot (voorskrif, vergroting, 'bp')
• hou vas
• rooster
• legende ('Data', 'Interpolated Points', 'Location', 'NW')

Ons kan 'n grafiek teken wat die vergrotingsverhoudings teenoor die gegewe voorskrif met 'n groen lyn toon en die gegewens van ons berekende vergroting teenoor ons geïnterpoleerde voorskrif met 'n blou ster. Dan merk die legende die titel, x-as en y-as en plaas die legende in die linker boonste hoek.

Stap 9: Beperk u voorskrif

Die volgende kode word gebruik om die afronding van die voorskrif te maak:

• as voorskrif <= 1.125

  CalculatedPrescription = '1.0';

• elseif Voorskrif <= 1.375

  CalculatedPrescription = '1.25';

• elseif Voorskrif <= 1.625

  CalculatedPrescription = '1.5';

• elseif Voorskrif <= 1.875

  CalculatedPrescription = '1.75';

• elseif Voorskrif <= 2.25

  CalculatedPrescription = '2.0';

• elseif Voorskrif <= 2.625

  CalculatedPrescription = '2.5';

• elseif Voorskrif <= 3

  CalculatedPrescription = '2.75';

• elseif Voorskrif <= 3.375

  CalculatedPrescription = '3.25';

• anders

  CalculatedPrescription = 'onbekend';

• einde

Die voorskrif wat deur middel van interpolasie gevind word, weerspieël nie noodwendig die werklike voorskrif nie - dit is omdat daar altyd klein variasies in die ontleding van die foto sal wees as gevolg van menslike foute. Ons het dus hierdie stap nodig om die werklike voorskrif te klassifiseer.

Die voorskrifte wat gegee word, begin gewoonlik by 1,0 diopters en styg met 0,25 in hul voorskrifte, dus na die berekening van die voorskrif wil ons die voorskrif bepaal wat die beste pas by wat die gebruiker nodig mag hê. Nadat ons die voorskrif bereken het, voer ons dit deur die gegewe If -stellings om die waarde daarvan na te gaan en te bepaal watter voorskrif nodig is. Enigiets kleiner as of gelyk aan 1.125, dan is die voorskrif 1.0. Enigiets kleiner as of gelyk aan 1.375, die voorskrif is 1.25. Enigiets kleiner as of gelyk aan 1.625, die voorskrif is 1.5. Enigiets kleiner as of gelyk aan 1.845, die voorskrif is 1.75. En so aan.

Die waardes neem toe namate ons kyk of die waardes kleiner is as. As ons die waardes afneem, dan sal die eerste as -stelling die eerste as -stelling die hele tyd lees. As die voorskrif die kleinste is, wil ons hê dat dit dit dadelik as die kleinste moet erken, daarom is die kleinste waarde waarmee ons begin het. Enigiets wat hoër is as die hoogste waarde, beteken dat die voorskrif nie binne die bereik van ons data is nie, dus gee dit die 'Onbekende' snaarlesing.