INHOUDSOPGAWE:
- Outeur John Day day@howwhatproduce.com.
- Public 2024-01-30 07:24.
- Laas verander 2025-01-23 12:53.
Rekursie is 'n baie nuttige en tyddoeltreffende prosedure wat 'n probleem vinnig kan oplos met baie min kode. Rekursie behels die metode wat u skep wat die oorspronklike probleem noem.
Vir hierdie voorbeeld sal ons 'n skikking van 10 heelgetalle saamvat, maar die grootte kan van enige lengte wees.
Voorrade
U moet die basiese java -sintaksis ken en u IDE of 'n teksredakteur hê om u kode vir hierdie taak te skryf.
Stap 1: Stel u hoofmetode op
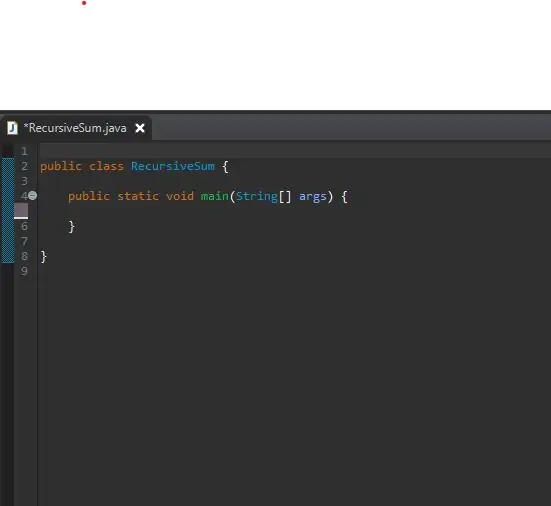
Om te begin, stel u hoofmetode op in 'n nuutgeskepte klas. Ek het my klas RecursiveSum genoem. Dit is waar u die skikking heelgetalle sal skep en u rekursiewe metode sal noem.
Stap 2: Skep u kop vir rekursiewe metode
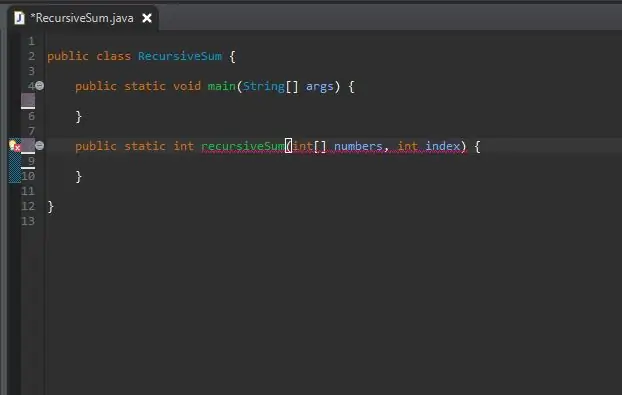
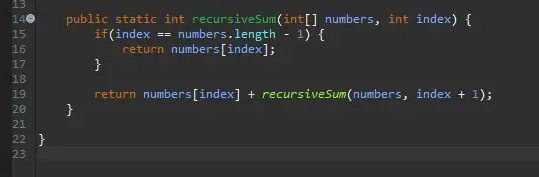
Buiten die hoofmetode, skep die metodeopskrif vir u rekursiewe metode.
Die metode is staties, aangesien dit nie van 'n voorwerp benodig om dit te gebruik nie.
Die tipe opgawe is int, aangesien die skikking wat ons gaan gebruik, vol is op heelgetalle. Dit kan egter verander word na watter getalletipe die skikking ook al bevat.
Ek het my metode recursiveSum genoem, wat twee parameters sal neem; 'n verskeidenheid heelgetalle en die indeks wat ons by die som sal voeg. Ek het hierdie parameters onderskeidelik getalle en indeks genoem.
U sal nou foute sien, en dit is goed. Hulle sal later reggestel word.
Stap 3: Skep u Kicker/basiskas
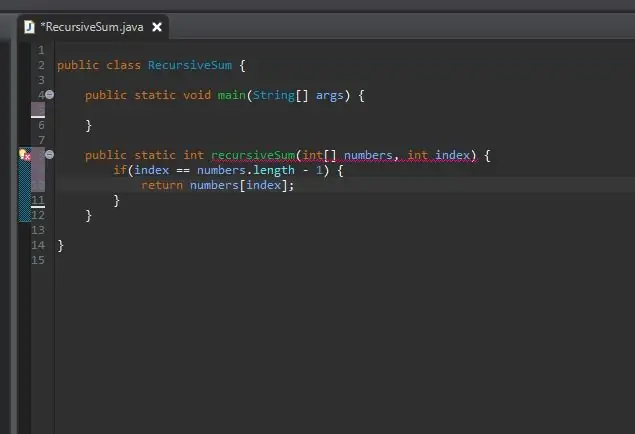
'N Rekursiewe metode benodig 'n skop-/basiskas. Dit is die toestand wat u metode sal keer om homself oneindig te noem. Hierdie basiese saak kan beskou word as die eenvoudigste geval wat ons sal teëkom. In hierdie geval is die basiese geval wanneer ons aan die einde van ons skikking is. As die huidige indeks gelyk is aan die lengte van die skikking (minus 1 omdat skikkings begin tel van 0 nie 1 nie), is ons aan die einde en gee ons die element eenvoudig by die indeks terug.
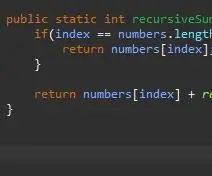
Stap 4: Die rekursiewe stap
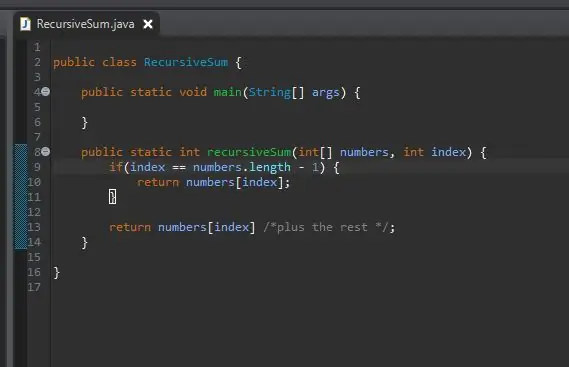
Sodra ons ons basiese saak het, is die volgende stap ons rekursiewe stap. Dit is waar die magie gebeur. Ons het die saak hanteer toe ons indeks gelyk is aan die laaste element in ons skikking. Wat as ons nie by die laaste element in ons skikking is nie? Wat as ons dit net kon sê om ons huidige element plus die volgende by te voeg? Uiteindelik sal ons die einde van ons reeks bereik, en ons basiese saak sal van invloed wees.
Om dit te bereik, gee ons eenvoudig ons huidige indeks terug en "voeg die res by" van die skikking.
Stap 5: Verkort die probleem
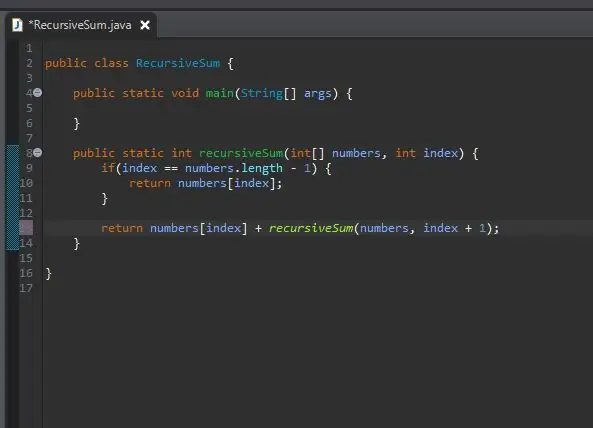
Hoe "voeg ons die res by"? Ons het reeds 'n metode wat 'n sekere element sal byvoeg; ons metode rekursiveSum ()! Ons kan dit weer noem, maar verander watter indeks ons som.
Ons slaag in dieselfde skikking wat ons verwerk, maar ons slaag die volgende indeks in van ons huidige indeks. Ons doen dit deur eenvoudig een by ons huidige indeks te voeg, soos getoon.
Stap 6: Skep die reeks heelgetalle
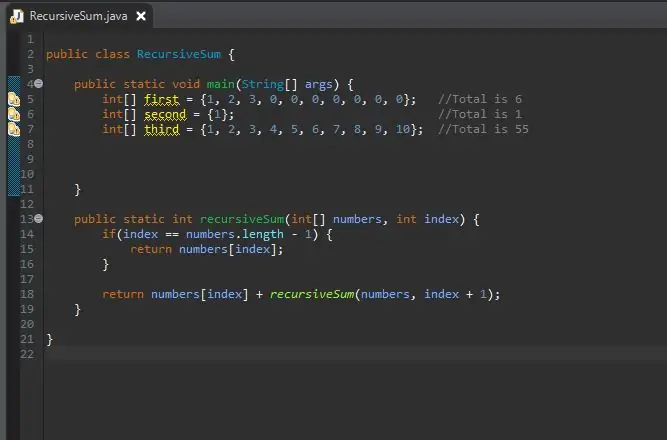
Noudat ons rekursiewe sommetode voltooi is, kan ons ons skikking skep wat ons sal verwerk. Hierdie skikking sal in ons belangrikste metodeblok voorkom.
U kan die grootte van die skikking so lank maak as wat u wil. Ek het 'n paar verskillende skikkings met verskillende groottes en waardes gemaak om aan te toon dat dit nie net op 'n enkele grootte werk nie.
Stap 7: Bel die metode met u skikkings
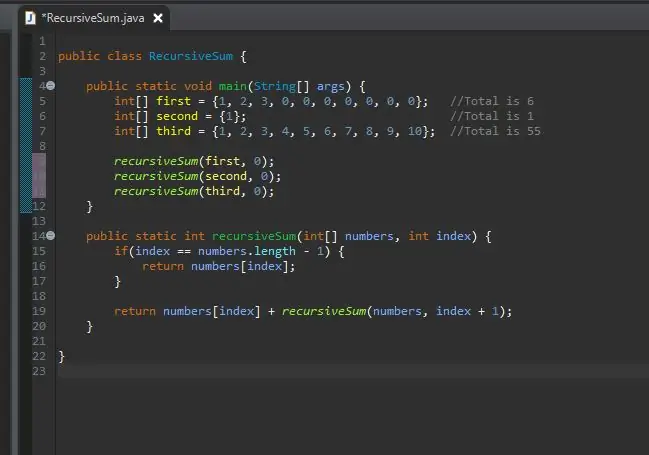
Nou kan u u rekursiewe metode skakel en hierdie skikkings daaraan deurgee. Nou kan u u program uitvoer.
Stap 8: Druk die resultate af
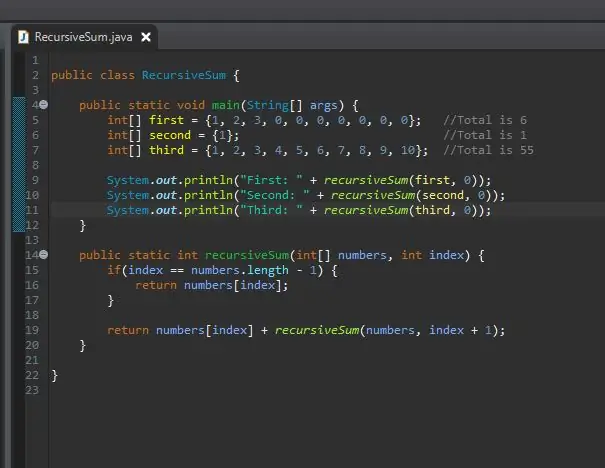
Niks het gebeur nie. Hoekom? Rekursiewe som gee 'n heelgetal op, maar ons het niks met hierdie heelgetal gedoen nie. Dit het sy werk gedoen, maar ons kan nie die resultaat sien nie. Om die resultaat te sien, druk ons dit eenvoudig so uit. Nadat u dit uitgevoer het, behoort u die resultate vir elk van u skikkings te sien.
Stap 9: Baie geluk
U het 'n rekursiewe funksie voltooi. Verander gerus die grootte van u skikkings. As u dit toets, sal u agterkom dat dit ineenstort as u 'n leë skikking het. Ons het dit nie verantwoord nie, maar dit is 'n uitstekende manier om u rekursiewe metode te verbeter.
Aanbeveel:
DIY LED Array (met behulp van Arduino): 7 stappe

DIY LED Array (met behulp van Arduino): INLEIDING: wou u al ooit 'n eenvoudige projek maak waarmee LED's beweeg? Geen? Dit is wat ek gedink het. As u ooit iets soortgelyks wou maak, is u op die regte plek
Smart Boei [opsomming]: 8 stappe (met foto's)
![Smart Boei [opsomming]: 8 stappe (met foto's) Smart Boei [opsomming]: 8 stappe (met foto's)](https://i.howwhatproduce.com/images/001/image-657-4-j.webp)
Smart Buoy [Summary]: Ons is almal mal oor die see. As 'n kollektief kom ons daarheen vir vakansies, om watersport te geniet of om 'n bestaan te maak. Maar die kus is 'n dinamiese gebied aan golwe. Stygende seevlakke knibbel aan strande en kragtige uiterste gebeurtenisse soos storm
Hoe om 'n while -lus te gebruik om 'n array in Java te herhaal: 9 stappe

Hoe om 'n while -lus te gebruik om 'n array in Java te herhaal: Vandag sal ek u wys hoe u Java kan gebruik om 'n While -lus te skep wat gebruik kan word om deur 'n lys getalle of woorde te herhaal. Hierdie konsep is vir programmeerders op intreevlak en vir almal wat Java Loops en skikkings vinnig wil opruim
OPSOMMING VAN AUTOMATIESE LIGBRON MET ARDUINO UNO R3: 5 stappe
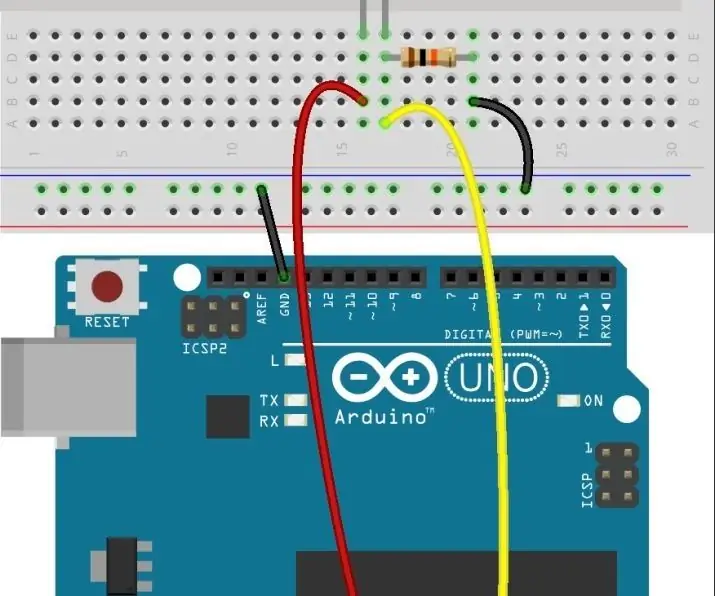
AUTOMATIESE LIGBRONVOERING MET ARDUINO UNO R3: In hierdie les gebruik ons 'n servomotor, 'n fotoresistor en 'n aftrekweerstand om 'n outomaties opspoorbare ligbronstelsel saam te stel
Opsomming: 3 stappe

Opmerking: dit is 'n uittreksel van 'n projek wat meer bevat as die voorwerpe. Hier konsentreer ek op materiaalkombinasies, insluitend beton
