Weet u van ESP32 ADC -aanpassing ?: 29 stappe

2024 Outeur: John Day | [email protected]. Laas verander: 2024-01-30 07:26

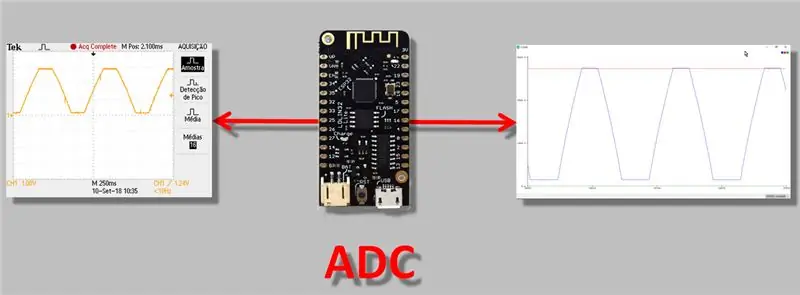
Vandag gaan ek praat oor 'n meer tegniese probleem, maar een wat ek dink almal wat met ESP32 werk, moet weet: die probleem van ADC (analoog-na-digitale omskakelaar) leesaanpassing. Ek vind dit belangrik, want as u 'meting' doen, veral met 'n instrument met 'n analoog uitset, moet u absoluut seker wees dat die lesing korrek uitgevoer word.

In die video vandag, sal ons dus metings doen met behulp van die "analoog-digitale omskakelaar" van die ESP32, die omskakelingsverskille waarneem en 'n ADC-aanpassings- / kalibreringsmetode toepas.

Stap 1: Wat is 'n AD -omskakelaar?

'N AD -omskakelaar is 'n stroombaan wat 'n analoog (deurlopende) hoeveelheid in digitale (diskrete) waardes kan vertaal. Wat beteken dit? Dit beteken dat hoewel digitale waardes slegs diskrete waardes kan aanneem wat gevorm word deur die kombinasie van nulle en ene, 'n analoog hoeveelheid enige waarde binne 'n reeks kan aanneem. Byvoorbeeld, as ons die spanning van 'n ideale AA -sel gemeet het, kan ons enige waarde tussen 0V en 1.5V vind, aangesien dit analoog is. Die uitgangstoestand van 'n ideale lamp moet slegs twee toestande aanneem (af of aan), wat 'n diskrete grootte is. Aangesien mikrobeheerders hierdie diskrete logika gebruik, benodig ons 'n stroombaan wat 'n analoog hoeveelheid in digitale (of diskrete) kan vertaal.

Stap 2: Hulpbronne gebruik

• Een Lolin32 Lite -kaart v1.0.0

• 'n Tektronix TDS1001C -ossilloskoop vir opname

• Een USB -kabel vir die ESP32

• 'n Hantek DSO4102C -ossilloskoop as seingenerator

Stap 3: ESP32 ADC

Volgens die Espressif-data kan die ESP32-skyfies 'n verskil van +/- 6% van die een na die ander in die gemete resultate lewer.

Boonop het die omskakeling NIE 'n lineêre antwoord vir elke beskikbare reeks om te lees nie. Espressif bied 'n kalibreringsmetode en stel voor dat gebruikers ander metodes implementeer as hulle dit nodig ag om die gewenste akkuraatheid te bereik.

Ons sal 'n data -verkryging uitvoer, en hieruit sal ons die ADC -antwoorde wys en 'n voorbeeld van die toepassing van 'n wiskundige proses om die aanpassing te lees.

Daar is verskeie (eenvoudiger of meer ingewikkelde) maniere om hierdie oplossings uit te voer. Dit is aan u om die geskikste vir u projek te evalueer.

Die een wat hier getoon word, sal 'n illustratiewe doel hê en probeer om interessante punte aan te spreek wat tydens aanpassings waargeneem kan word.

Stap 4: Kring gebruik

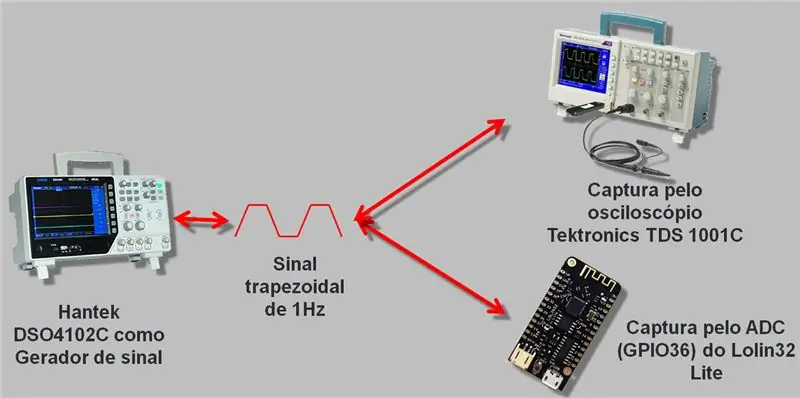
Ek het 'n ossilloskoop gebruik met 'n seingenerator wat tot 25 MHz, die Hantek DSO4102C, styg. Ons het 'n golf genereer wat deur die ESP A / D en die ossilloskoop gelees is. Die versamelde data is opgeneem in csv en in 'n sigblad, wat ek aan die einde van die artikel sal laat aflaai.

Stap 5: Teken gebruik

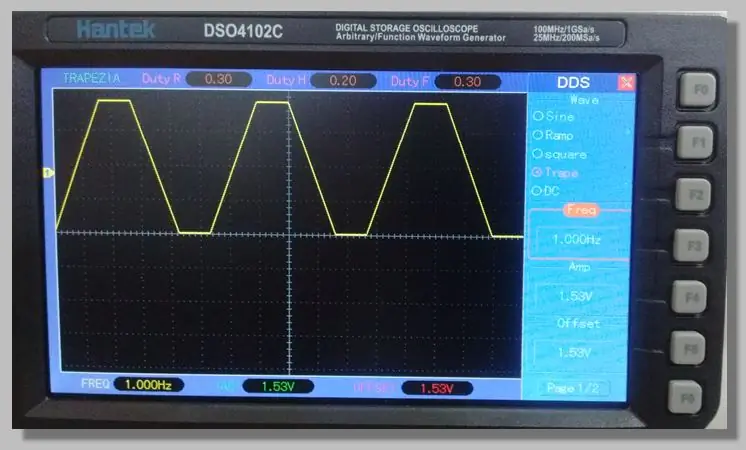
Ons het 'n trapeziumvormige sein met 'n lae frekwensie gekies wat toegang bied tot die opritte wat deur die hele omskakelingsreeks loop. Dit maak 'n groot aantal monsters op hierdie opritte moontlik.

Stap 6: Data verkry deur die ossilloskoop

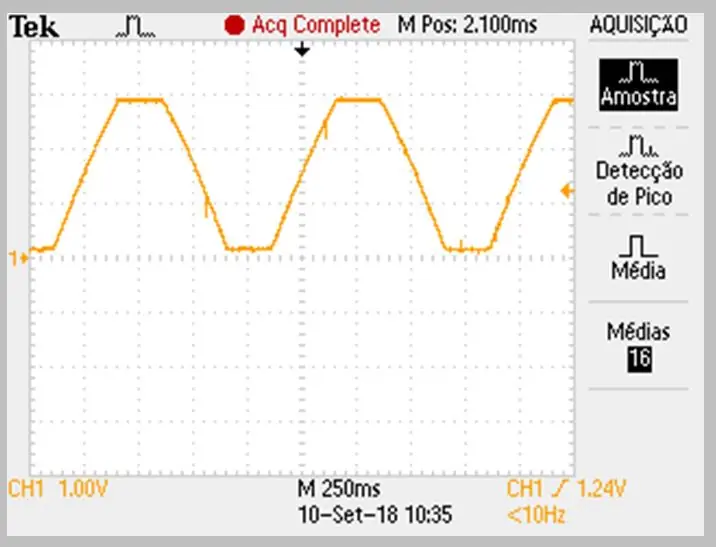
Die beeld van die opname is uitgevoer deur die ossilloskoop. Die data is in 'n csv -lêer gestoor. Let op die geringe kromming op die stygende en dalende opritte van die sein.

Stap 7: Data verkry deur die oscilloskoop (csv -lêer in Excel)

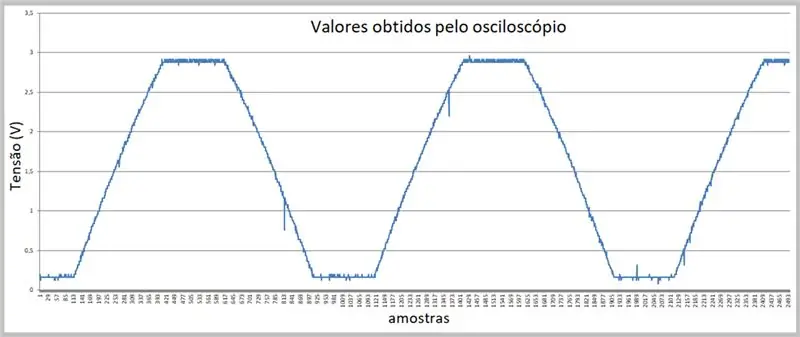
Ons het die steekproewe hier.

Stap 8: Data verkry deur die ADC

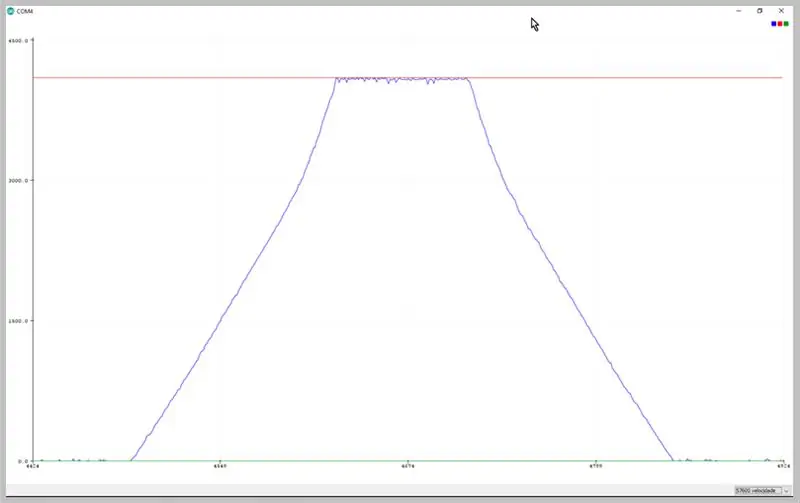
Deur die oordragkoers van die reeks te verander, kan ons die data wat deur die ADC vasgelê is, sien. Let op die vervorming van die trapeziumvormige sein.

Data waargeneem op die Arduino IDE -reeksplotter

Stap 9: Data verkry deur ADC - Excel

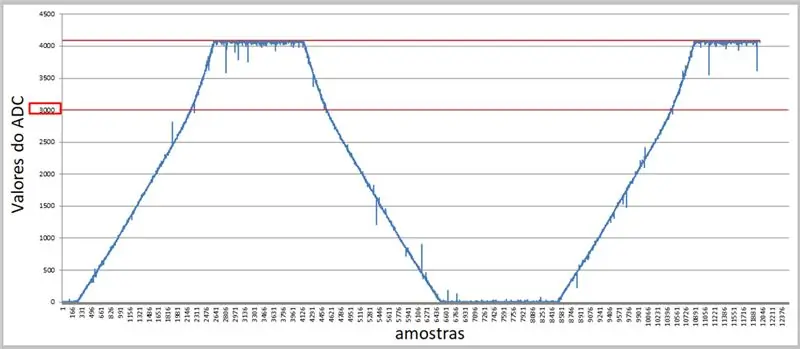
Deur 'n hoër koers en die seriële terminaal te gebruik, kan ons die waardes vaslê en in Excel toepas vir ons vergelykings.

Stap 10: Vergelyking van klimopritte

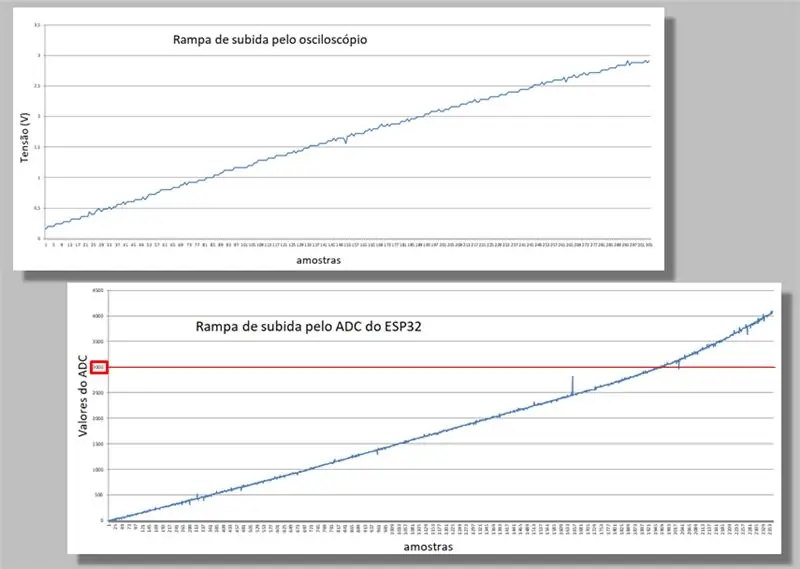
Ons vergelyk die twee klimritte van die twee vangs.

Let op die kromming wat op beide opritte voorkom.

Let ook daarop dat ons vir dieselfde oprit baie meer monsters van die ESP32 het as van die ossilloskoop.

Stap 11: Stel die aantal monsters gelyk

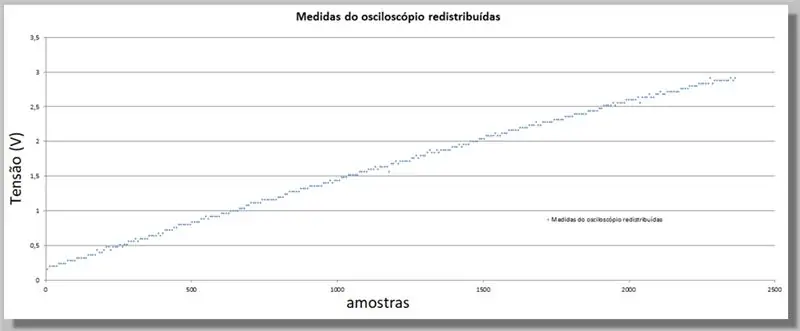
Omdat die ESP32 'n groter aantal monsters as die ossilloskoop verskaf het, moet ons hierdie waardes gelykstel, aangesien dit 'n indeks sal wees om die twee krommes te vergelyk.

Hiervoor sal ons 'n direkte vergelyking tref.

Ons het 305 monsters vir die ossilloskoopoprit en 2365 monsters vir die ADC -oprit.

Aangesien die opritte van dieselfde reeks is, kan ons sê dat ons ongeveer 7,75 monsters van die ADC vir elke ossilloskoop het.

Die vermenigvuldiging van die indeks van elke ossilloskoopmonster het dieselfde kromme, maar met indekse gelykstaande aan die ADC en die herverspreide data.

Om die ontbrekende data vir die nuwe posisies in te vul, pas ons 'n kromme toe wat statisties pas by die bekende data.

Stap 12: Vul die gapings - tendenslyn

Deur die bekende data (blou kolletjies) te kies, klik en klik dan met die regterknoppie: "Voeg trendlyn by …"

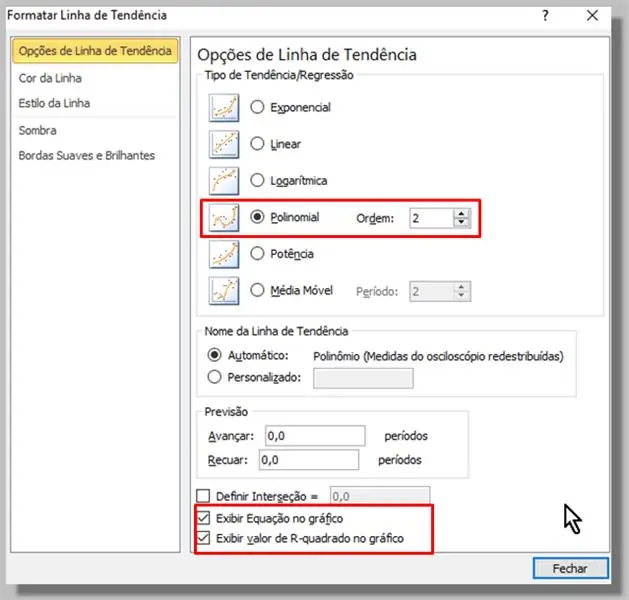
In die venster wat verskyn, kies ons die polinoom tipe (volgorde 2 is genoeg).

Ons het ook die opsies "Bekyk vergelyking in die grafiek" en "Vertoon R-kwadraatwaarde in die grafiek" nagegaan.

Ons klik op "Close".

Stap 13: Vul die gapings in - graad 2 polinoomkromme

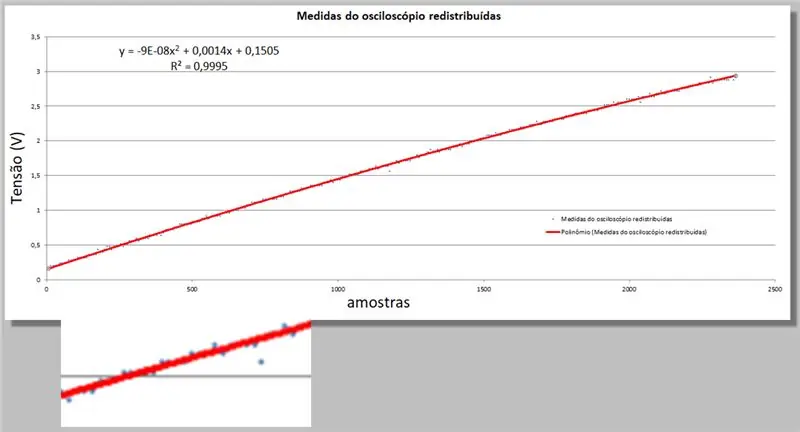
Excel gee ons twee nuwe inligting; die tweede orde vergelyking wat die beste by die data pas, en die R-kwadraat vergelyking wat hierdie toereikendheid kwantifiseer.

Onthou net dat hoe nader aan 1 die vergelyking meer gepas is.

Laat ons nie verdiep in die betrokke wiskunde nie; laat ons dit net as 'n instrument gebruik.

Stap 14: Die gapings vul - Evaluering van die funksie

Kom ons vul die steekproefgapings in met die data wat deur die vergelyking gegenereer word. En dan, vergelyk dit punt vir punt.

y = -9E -08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Oscilloskoop spanning = -9E -08 * indeks2 + 0, 0014 * indeks + 0, 1505

Stap 15: Omskakeling van die ossilloskoopspanning na 'n ekwivalente waarde om te vergelyk met die ADC

Kom ons neem voordeel hiervan om ook die waarde van die ossilloskoopspanning te omskep in 'n ekwivalente ADC -waarde.

Aangesien die hoogste waarde in die ADP van die ESP32 4095 was, wat gelykstaande is aan die lesing van 2.958V vir dieselfde indeks, kan ons sê dat:

Elke volt in die metings van die ossilloskoop is gelyk aan ongeveer 1384,4 eenhede van die AD. Daarom kan ons alle metings van die ossilloskoop met hierdie waarde vermenigvuldig.

Stap 16: Vergelyking van die verkreë twee rampe

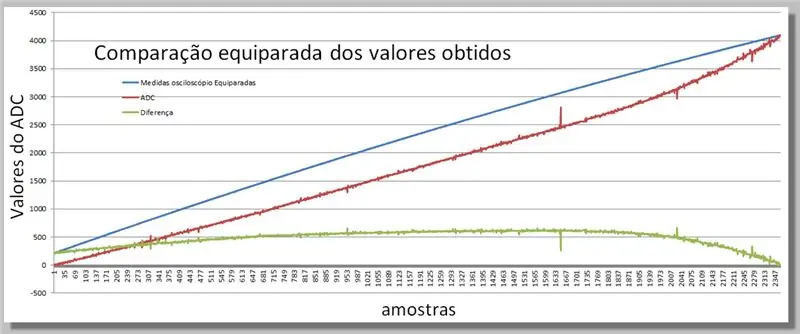
Visualiseer die verskille wat in die twee lesings verkry word.

Stap 17: Gedrag van die ADC Leesverskil (FOUT)

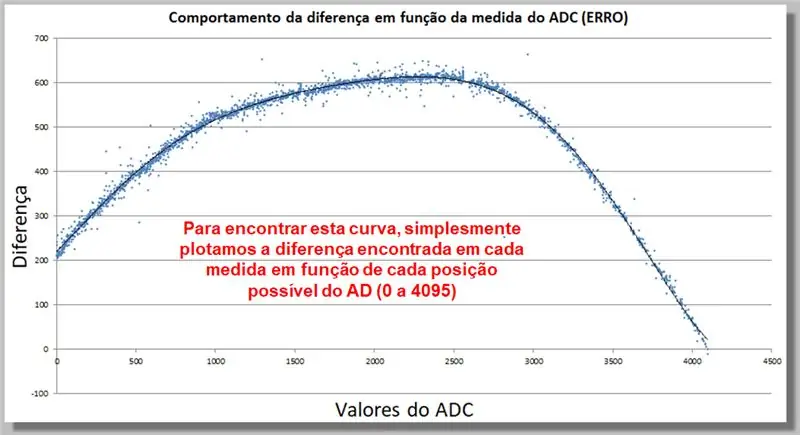
Die kromme hieronder toon hoe die verskil in die ADC -lesing optree as 'n funksie van die meting. Met hierdie versameling data kan ons 'n regstellingsfunksie vind.

Om hierdie kromme te vind, teken ons eenvoudig die verskil wat in elke maat gevind word as 'n funksie van elke moontlike AD -posisie (0 tot 4095).

Stap 18: ADC Leesverskilgedrag - vind 'n regstellingsfunksie

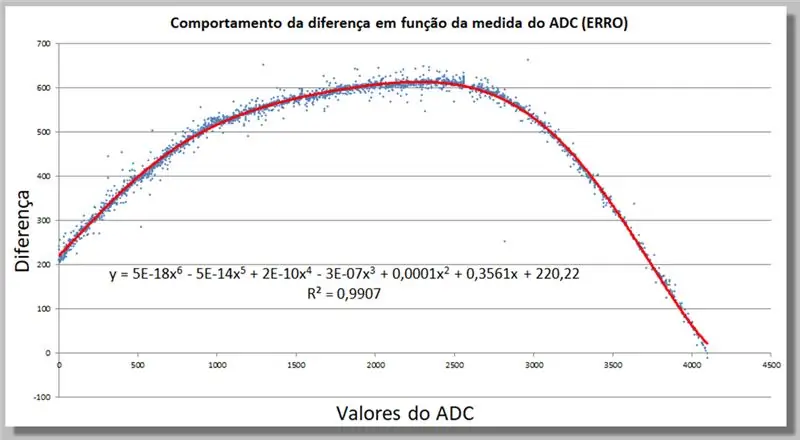
Ons kan 'n regstellingsfunksie in Excel bepaal deur 'n nuutste tendenslyn by te voeg totdat dit voldoende by ons data pas.

Stap 19: Gebruik ander sagteware

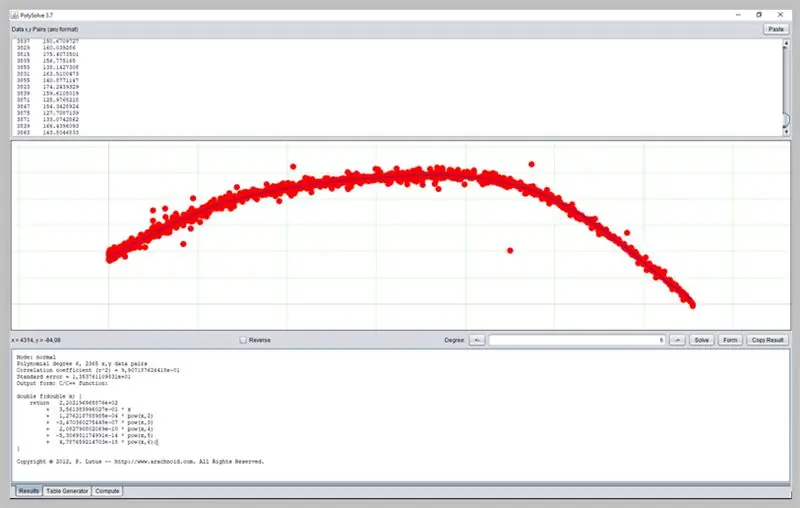
Ander interessante sagteware om krommes te bepaal, is PolySolve, wat direk op die skakel gebruik kan word: https://arachnoid.com/polysolve/ of afgelaai word as 'n Java -toepassing.

Dit laat die toepassing van hoërgraad-polinoom-regressies toe en die opmaak van die geformateerde funksie, sowel as ander funksies.

Om dit te gebruik, voer die data in die eerste tekskassie in. Die data moet die volgorde X, Y volg, geskei deur 'n komma of oortjie. Wees versigtig deur die punt korrek as 'n desimale punt te gebruik.

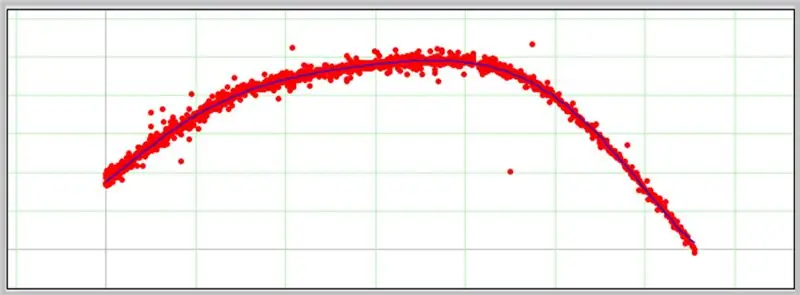
'N Grafiek sal in die volgende blokkie verskyn as die ingevoerde data korrek geformateer is.

Hier is hoe ons ADC -foutkurwe verloop het.

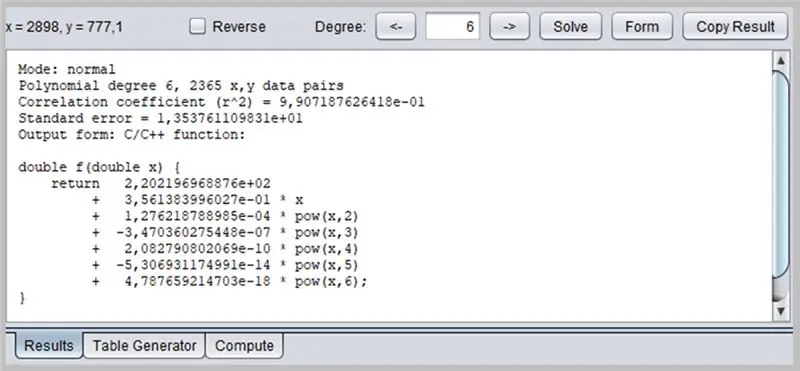
Hierdie venster bied die resultaat van die regressie, insluitend funksie -toereikendheidsdata, wat op sy beurt die uitvoer op verskillende maniere kan formateer: as 'n C / C ++ - funksie, 'n lys van koëffisiënte, 'n funksie wat in Java geskryf is, ens.

Let wel: let op desimale skeidings

Stap 20: Konstante en opstelling ()

Ek wys hier op die GPIO wat gebruik word vir analoog opname. Ek initialiseer die seriële poort, sowel as die pen wat bepaal is vir analoog opname.

const int pin_leitura = 36; // GPIO usado para captura analógica leemte opstelling () {Serial.begin (1000000); // Inisiciando a porta serial somente for debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

Stap 21: Loop () en die regstellingsfunksie

Ons bepaal die aangepaste spanning en druk die waardes af met of sonder die korrekte korreksies.

leemte -lus () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

Let op reël 12 dat ons die data kan druk met die byvoeging van die verskilfunksie f (analoog_waarde).

Stap 22: Gebruik die PolySolve -regstellingsfunksie

Hier gebruik ons die PolySolve -funksie in die Arduino IDE.

/* Modus: normale polinoomgraad 6, 2365 x, y datapare Korrelasiekoëffisiënt (r^2) = 9, 907187626418e-01 Standaardfout = 1, 353761109831e+01 Uitsetvorm: C/C ++-funksie: Kopiereg © 2012, P. Lutus - https://www.arachnoid.com. Alle regte voorbehou. */ dubbel f (dubbel x) {opgawe 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Let op die komma-vir-punt-verandering as die desimale skeier.

Stap 23: Vang met korreksie - Plotter Serial

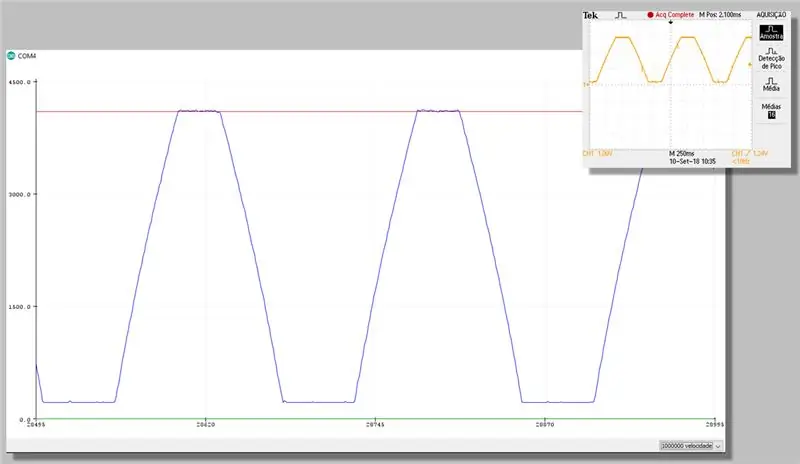
Stap 24: Berekeningskoste

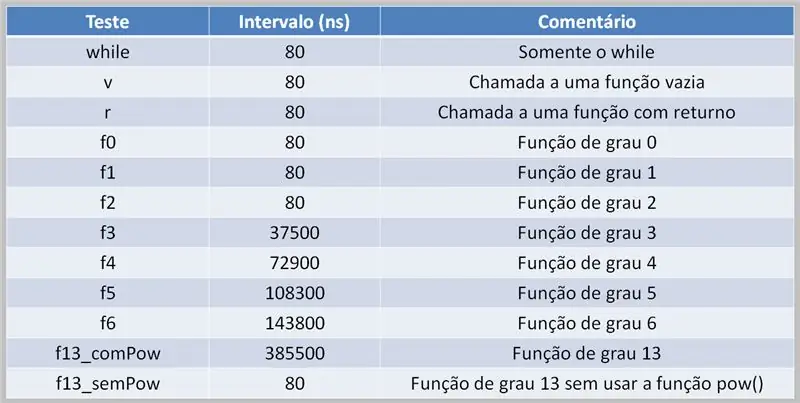
Om polinoomberekenings uit te voer, is dit nodig dat die verwerker hierdie taak hanteer. Dit kan lei tot vertragings in die uitvoering, afhangende van die bronkode en beskikbare rekenaarkrag.

Hier sien ons 'n resultattabel van 'n toets met behulp van meervoudige polinoom. Let op die verskil tussen die tye toe die pow () -funksie gebruik is en wanneer dit nie die geval was nie.

Stap 25: Toetskode - opstelling () en lus begin ()

Hier het ons die kode wat in ons toets gebruik is.

ongeldige opstelling () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // quantidade de chamadas float contador = 0.0; // contador de chamadas

Stap 26: Toetskode - lus () en verwerking

Ek het die funksie micros () gebruik om die waarde in mikrosekondes te kry.

// ============== inicia o processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / quantidade; // determina o intervalo que se passou para cada iteração // ============== finaliza o processo

Stap 27: Toetskode - Lus () - Resultate

Ons druk die waarde terug van die graad 13 -funksie met en sonder POW vir vergelyking, sowel as die verwerkingsinterval.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a função POW Serial.print (" -"); // imprime o intervalo do processamento Serial.println (agora, 6); }

Stap 28: Toetskode - gebruikte funksies

Leë funksies (slegs met terugkeer) van graad 0 en 1.

// FUNÇÃO VAZIDubbel v (dubbel x) {} // FUNÇÃO SOMENTE COM RETORNO dubbel r (dubbel x) {opgawe x; } // FUNÇÃO DE GRAU 0 dubbel f0 (dubbel x) {opgawe 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 dubbel f1 (dubbel x) {opgawe 2.202196968876e + 02 + 3.561383996027e-01 * x; }

Graad 2, 3 en 4 funksies.

// FUNÇÃO DE GRAU 2dubbel f2 (dubbel x) {opgawe 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 dubbel f3 (dubbel x) {opgawe 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)); } // FUNÇÃO DE GRAU 4 dubbel f4 (dubbel x) {opgawe 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4); }

Graad 5 en 6 funksies.

// FUNÇÃO DE GRAU 5dubbel f5 (dubbel x) {opgawe 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 dubbel f6 (dubbel x) {opgawe 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Graad 13 funksie met behulp van die POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdubbel f13_comPow (dubbel x) {opgawe 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

Graad 13 funksie sonder om POW te gebruik.

// FUNÇÃO DE GRAU SEM USAR O POWdubbel f13_semPow (dubbel x) {opgawe 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Stap 29: lêers

Laai die lêers af:

PDF

EK NEE

Sigblad