
INHOUDSOPGAWE:
- Outeur John Day day@howwhatproduce.com.
- Public 2024-01-30 07:29.
- Laas verander 2025-01-23 12:53.
Hierdie instruksies dek enkele van die mees basiese funksies van matlab. U sal leer hoe om matlab intern en plot 'n periodieke funksie te laat funksioneer, en hoe u dieselfde periodieke funksie uit 'n Excel -lêer kan trek en dit kan plot. Hierdie funksies is van die mees basiese en word wyd gebruik in matlab. Hierdie instruksies is gerig op diegene onder u wat nog nooit matlab gebruik het nie en net 'n paar eenvoudige take daarmee moet uitvoer. Die kode wat op elke prent uitgelig is, word as 'n opmerking ingesluit, sodat u die kode kan kopieer en plak. Neem gerus hierdie kode en verander dit om by u aansoek te pas.
Stap 1: Begin Matlab
Die eerste stap is om matlab aan die gang te kry sodat ons daarmee kan begin werk. As u die eerste keer met matlab begin, moet dit soos die kiekie hieronder lyk. Die eerste stap is om 'n gids vir matlab toe te ken om van te werk. Dit is waar die program al die lêers vandaan sal haal en dit is waar u al u matlab -werk moet stoor. Sodra u 'n nuwe gids gemaak het, klik op die "…" regs bo in die skerm, soos in die tweede prent uitgelig. Dit sal 'n blaaier oopmaak soos in die derde prentjie. Soek die nuwe gids wat u op u rekenaar geskep het en kies dit. In hierdie voorbeeld word die lêer '370' genoem en is op die lessenaar geleë.
Stap 2: Skep 'n M-lêer
Wat ons nou moet doen, is om 'n nuwe M -lêer te skep. 'N M -lêer funksioneer presies soos om kode direk in matlab in te tik, maar u kan die kode stoor en verander en herhaaldelik laat loop. As u kode direk in matlab invoer, tik u elke reël kode afsonderlik. In 'n M -lêer skryf u u hele kode en voer dit dan dadelik uit. Om 'n nuwe M -lêer oop te maak, klik op lêer. Plaas die wyser op "New" en klik dan op "Blank M -lêer" soos in die eerste prentjie getoon. Wat oopmaak, moet soos die tweede prentjie lyk. Aangesien hierdie kode herhaaldelik uitgevoer kan word, is dit 'n goeie idee om alles te sluit en al die veranderlikes skoon te maak voordat dit elke keer uitgevoer word. Dit word bewerkstellig deur middel van twee reëls kode: sluit alles, maak alles skoon Soos gesien in die derde prentjie, verseker dat alles skoongemaak en gesluit is.
Stap 3: Skep 'n tydsvektor
Die eerste ding wat ons sal doen, is om 'n grafiek van 'n funksie in matlab te skep. Die eerste stap is om die onafhanklike veranderlike te skep. In hierdie geval sal ons dit vir tyd "t" noem. Die metode wat ons sal gebruik om hierdie veranderlike te skep, is om 'n vektor te maak. 'N Vector is basies 'n reeks getalle. Byvoorbeeld, 1, 2, 3, 4 sou 'n kort vektor wees. Die kode om hierdie vektor te skep is: t = 0.1: 0.01: 10; Die eerste getal, 0.1, verwys na die beginpunt. Die tweede getal, die 0.01, verwys na die stapgrootte. Die derde getal, 10, verwys na die eindpunt. Hierdie vektor stem dus ooreen met 0.1, 0.11, 0.12 … tot en met 10. Om te sien of die vektor geskep is, klik op die groen run -knoppie wat in die tweede prentjie gemerk is. Dit loop die program. Gaan na die hoof matlab venster om ons vektor te sien. Klik op die lessenaar, dan met die muis oor die lessenaaruitleg, en klik dan op die standaard soos uiteengesit in die derde prentjie. Nou moet u skerm soos die vierde prentjie lyk. Aan die regterkant sien u ons nuutgeskepte veranderlike, t. Dubbelklik daarop en soos in die vyfde prentjie, sien u die reeks getalle wat geskep is.
Stap 4: 'n Funksie uitvoer en teken
Nou teken ons 'n grafiek van 'n funksie wat in matlab geskep is. Die eerste stap is om die funksie te skep. Dit is so eenvoudig soos om die gewenste wiskundefunksie uit te skryf. 'N Voorbeeld word in die eerste prentjie getoon. Die kode wat vir hierdie funksie gebruik word, is: y = sin (t)+4*cos (5.*t).^2; Die tydperk voor die vermenigvuldiging in die kosinus, en voor die kwadraat van die kosinus, vertel matlab om die funksies uit te voer bloot op die waardevolle items van die tydsvektor, nie om die tydvektor as 'n matriks te behandel nie en probeer om matriksfunksies daarop uit te voer. Die volgende stap is om die figuur self te skep. Dit word bewerkstellig met behulp van die kode in die tweede figuur. Die volgorde van die veranderlikes in die plotopdrag is baie belangrik, dus maak seker dat u u kode opstel net soos dit hieronder opgestel is. xlabel ('Tyd (e)') ylabel ('Y -waarde') Titel ('Y -waarde vs tyd') -rooster Aan, klik uiteindelik weer op die groen lopie -pyltjie, en die syfer moet verskyn soos in die derde prentjie.
Stap 5: haal data uit Excel
Ons sal nou dieselfde grafiek as voorheen skep, maar deur die funksiedata uit 'n Excel -sigblad in te voer. Die eerste prentjie is 'n skermkiekie van die Excel -sigblad wat gebruik sal word. Dit is presies dieselfde datapunte wat in die vorige stappe in matlab geskep is, net in excel gemaak. Om mee te begin, kan ons die kode wat ons tydsvektor en die kode vir ons funksie skep, uit die vorige stappe verwyder. U kode moet nou soos die tweede prentjie lyk. Plaas die kode soos in die boonste rooi blokkie van die derde prentjie. Dit is die kode om die Excel -lêer te lees. "A" verwys na 'n matriks wat al die getalle in die sigblad bevat, en "B" bevat al die teks uit die sigblad. Die t en y veranderlikes word uit die eerste en tweede kolom getrek soos in die kode getoon. [A, B] = xlsread ('excelexample.xlsx'); t = A (:, 1); y = A (:, 2); Die figuurkode kan ook gewysig word soos getoon in die onderste rooi blokkie op die derde prentjie. Dit trek eintlik die grafiek titel en as etikette uit die sigblad en plaas dit op u grafiek. Etiket (B (2)) ylabel (B (3)) Titel (B (1)) weer, en u sien dieselfde figuur verskyn soos in die finale prentjie.
Stap 6: Skep 'n Specgram
In hierdie stap gebruik ons matlab om 'n specgram te maak deur 'n wav -klanklêer te lees. 'N Specgram word soms 'n' 2.5D -grafiek 'genoem, omdat dit 'n tweedimensionele grafiek gebruik, met die byvoeging van kleur om amplitude aan te toon. Die kleur bied meer besonderhede as 'n eenvoudige 2D -grafiek, maar nie die detail van 'n 3D -grafiek nie, vandaar die term "2.5D." Die specgram -funksie van matlab neem 'n stel datapunte uit die wav -lêer en voer 'n Fourier -transformasie uit op die punte om die frekwensies wat in die sein voorkom, te bepaal. Vir hierdie instruksies, is dit nie belangrik om te weet hoe 'n Fourier -transformasie werk nie, maar weet dat die specgram die frekwensies van die frekwensie aanwys en hoe sterk dit is ten opsigte van tyd. Die funksie teken tyd op die X-as en frekwensie op die Y-as. Die sterkte van elke frekwensie word deur kleur vertoon. In hierdie geval is die wav -lêer 'n klankopname van 'n stuk metaal wat geslaan word, en dan word die trillings van die metaal as klank opgeteken. Met behulp van die specgram kan ons die resonante frekwensie van die metaalstuk maklik bepaal, want dit is die frekwensie wat die langste met die tyd aanhou. Om hierdie taak uit te voer, moet u eers die wav -lêer deur matlab lees deur die volgende kode te gebruik: [x, fs] = wavread ('flex4.wav'); In hierdie geval is flex4.wav die titel van ons wav -lêer, die veranderlike x is die datapunte in die lêer, en fs verwys na die bemonsteringsfrekwensie. Om die specgram uit te voer, tik net die volgende kode: specgram [x (:. 1), 256, fs]; Die 256 stem ooreen met die frekwensie waarop die FFT uitgevoer word tydens die ontleding van die data. Matlab kap basies die klanklêer in stukke en neem 'n FFT op elke stuk. Die 256 vertel hoe groot elke stuk moet wees. Die besonderhede hiervan is nie belangrik nie, en 256 is 'n veilige waarde om vir die meeste toepassings te gebruik. As u nou die kode gebruik, sal u 'n figuur sien verskyn soos in die tweede prentjie. Hieruit is dit maklik om te sien dat die resonante frekwensie ooreenstem met die rooi piek in die onderste regterhoek van die figuur. Dit is die hoogtepunt wat die langste met betrekking tot tyd aanhou.
Aanbeveel:
Reckless Racer Arduino OLED Game, AdafruitGFX en Bitmaps Basics: 6 stappe

Reckless Racer Arduino OLED Game, AdafruitGFX en Bitmaps Basics: In hierdie tutoriaal gaan ons kyk na hoe om bitmaps te gebruik met behulp van Adafruit_GFX.c biblioteek as 'n soort sprites in 'n speletjie. Die eenvoudigste speletjie waaraan ons kan dink, is 'n kant -en -weer -wisselende motorspeletjie, uiteindelik is ons beta -toetser en assistentkodeerder
Transistor Basics - BD139 & BD140 Kragtransistor Tutoriaal: 7 stappe

Transistor Basics | BD139 & BD140 Kragtransistor -tutoriaal: Hey, wat gaan aan, ouens! Akarsh hier van CETech af. Vandag gaan ons 'n bietjie kennis kry oor die kragstasie van die klein, maar baie groter in werk -transistorkringe. Basies gaan ons 'n paar basiese beginsels bespreek wat verband hou met die transistors en
Animatronics Basics - die servomotor: 8 stappe

Animatronics Basics - die Servomotor: Of dit nou 'n vrolike vakansievertoning in die venster van 'n winkel is, of 'n eng Halloween -grap, niks trek aandag soos 'n geanimeerde marionet nie. Hierdie elektronies beheerde animasies word soms " animatronics " en dit
IoT Basics: Koppel u IoT aan die wolk met behulp van Mongoose OS: 5 stappe

IoT Basics: Koppel u IoT aan die wolk met Mongoose OS: as u 'n persoon is wat besig is met knoeiery en elektronika, kom u die term Internet of Things, gewoonlik afgekort as IoT, teë, en dit is verwys na 'n stel toestelle wat met die internet verbind kan word! Om so 'n persoon te wees
RC522 en PN532 RFID Basics: 10 stappe
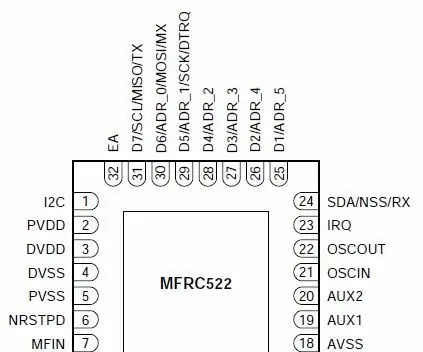
RC522 en PN532 RFID Basics: OPMERKING: ek het nou instruksies wat Arduino -kode vir die RC522 en PN532 bied. 'N Ruk gelede het ek drie verskillende RFID -modules gekoop om te eksperimenteer. In 'n vorige projek het ek uiteengesit hoe ek 'n eenvoudige 125 kHz-module kan gebruik om 'n basiese beveiligingsfunksie te doen
