Blink Caos: Mapa Logístico Para Random Blink: 5 stappe

2024 Outeur: John Day | [email protected]. Laas verander: 2024-01-30 07:24

Este es un instructable para un generador de aleatoriedad, utilizando un mapa logístico, que ahora explico que es. Met 'n logistieke kaart, kan u 'n lidmaatskap van die voorblad sien. Este puede servir simplemente de ejemplo de como a través del caos se generan comportamientos aparentemente aleatorios. Nee, dit is 'n goeie idee, maar ek kan dit ook doen

Stap 1: materiaal

Ocupamos:

1. Arduino UNO
2. Broodbord
3. Kabels
4. Led
5. Potensiaal van 10k Ohm

Stap 2: Conexiones

Ons het ook al pin 13 (pata larga) y a tierra (pata corta). In die pen 13, is daar geen weerstand nie.

Ons kan ook 'n "5V" la pata izquierda, 'n "GND" la pata derecha, 'n la del centro a A0.

Eso es todo!

Stap 3: Mapa Logístico

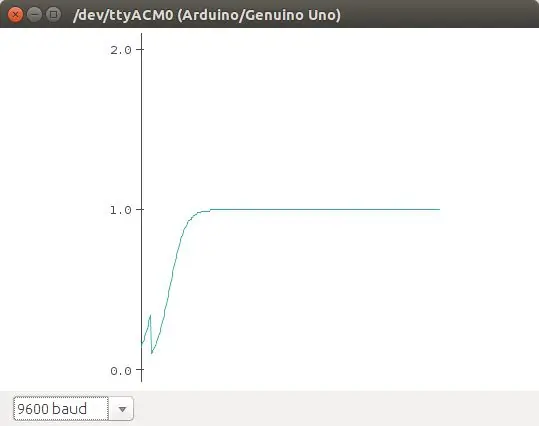
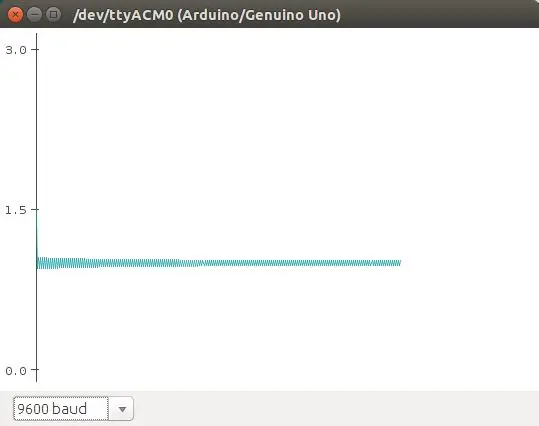
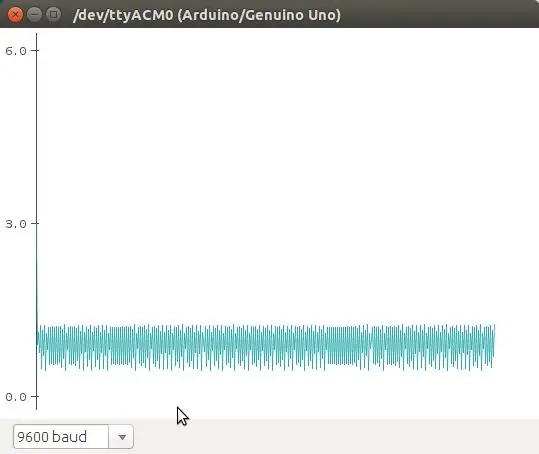
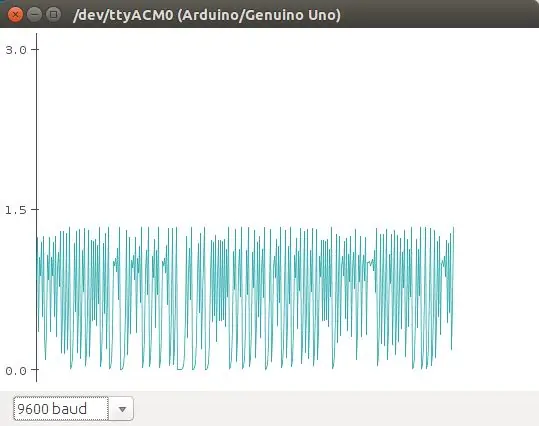
Die logistieke kaart is een van die belangrikste eienskappe wat 'n logistieke logistiek kan beskryf. Dit is een van die mees uiteenlopende aspekte wat ons kan herhaal, en ons kan dit herbereken. Esta ecuación muestra como comportamiento caótico puede emerger de una ecuación tan simple. Fue popularizada por Robert May en 1976. La ecuación:

n (t+1) = r * n (t) * (1 - n), beskryf a la población en t+1, como una función de la población en t, multiplicado por su potencial biótico (como se reproduce), y un efecto denso -dependiente que se introduce en el término (1 - n). Esta es la versión normalizada de la ecuación. Básicamente, debido al termino (1 - n), la población crece si n> 1, y decrece n <1.

En este eemplo vamos a utilizar como punto crítico cuando la población n> 1, que se encienda el led. El potenciómetro se utiliza para cambiar los valores de r en la ecuación.

Ons kan ook 'n volledige kombinasie van e -posse (graficados con el plotter de Arduino) sien.

Ons kan nie meer 'n logistieke kaart op wikipedia gebruik nie

Stap 4: Verwerk

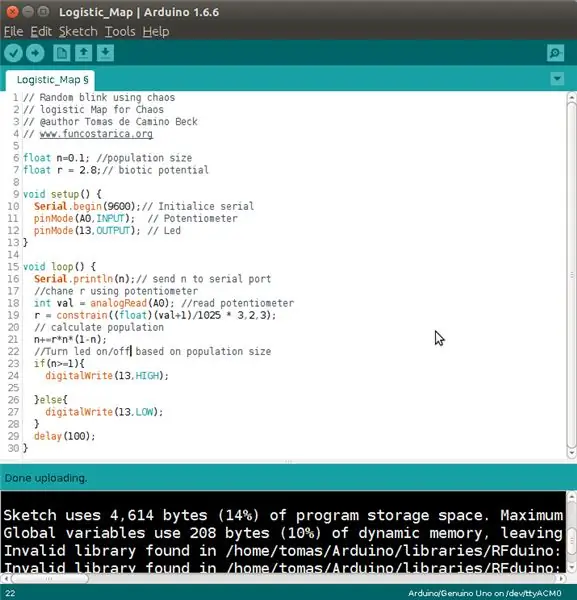
Ons kan die belangrikste programme van die program (lus) gebruik, en ek kan dit ook gebruik om 'n logistieke kaart te gebruik. En las líneas 6 y 7 se definen dos variables globales n para el tamaño de población y r para potencial biótico.

En la línea 18 se lee el potenciómetro, y en la 19, se convierte, primero a una escala de valor entre 0 y 1, y luego a un valor entre 0 y 3, aunque a eso se le aplica "constrain", para limitar los tipos de comportamiento que quiero con el potenciómetro (hay varias maneras de hacerlo y esta probablemente no es la mejor)

De las líneas 23 a la 28 simplemente se decid cuando prender el led.

Laai die kaart af om dit te laai.

Stap 5: Funcionando

As 'n algemene verloop van die funksie van 'n oscilaciones periódicas, kan ons 'n enkele keer 'n oogwink neem.

Ons kan dit ook gebruik om 'n paar verskillende generasies van verskillende tye te gebruik.