Eenvoudige outomatiese kondensator -toetser / kapasiteitsmeter met Arduino en met die hand: 4 stappe

2024 Outeur: John Day | [email protected]. Laas verander: 2024-01-30 07:26

Hallo!

Vir hierdie fisika-eenheid benodig u:

* 'n kragtoevoer met 0-12V

* een of meer kapasitors

* een of meer laaiweerstands

* 'n stophorlosie

* 'n multimeter vir spanningsmeting

* 'n arduino nano

* 'n 16x2 I²C -skerm

* 1 / 4W weerstande met 220, 10k, 4.7M en 1Gohms 1 gohms weerstand

* dupont draad

Stap 1: Algemene inligting oor kondensators

Kondensators speel 'n baie belangrike rol in elektronika. Hulle word gebruik om ladings te stoor, soos 'n filter, integrator, ens. Maar wiskundig is daar baie in kapasitors. U kan dus eksponensiële funksies met kondensators oefen. uitwerk. As 'n aanvanklik ongelaaide kondensator via 'n weerstand aan 'n spanningsbron gekoppel is, vloei ladings voortdurend na die kapasitor. Met die toenemende lading Q, volgens die formule Q = C * U (C = kapasitansie van die kapasitor), neem die spanning U oor die kapasitor ook toe. Die laadstroom neem egter al hoe meer af namate die vinnig gelaaide kondensator al hoe moeiliker word om met ladings te vul. Die spanning U (t) op die kapasitor volg die volgende formule:

U (t) = U0 * (1-exp (-k * t))

U0 is die spanning van die kragtoevoer, t is die tyd en k is 'n maatstaf van die spoed van die laaiproses. Van watter groottes hang k af? Hoe groter die bergingskapasiteit (dit wil sê die kapasitansie C van die kondensator), hoe stadiger word dit gevul met ladings en hoe stadiger word die spanning. Hoe groter C, hoe kleiner k. Die weerstand tussen kapasitor en kragtoevoer beperk ook laadvervoer. 'N Groter weerstand R veroorsaak 'n kleiner stroom I en daarom vloei minder ladings per sekonde na die kapasitor. Hoe groter R, hoe kleiner k. Die korrekte verhouding tussen k en R of C is:

k = 1 / (R * C).

Die spanning U (t) by die kapasitor neem dus toe volgens die formule U (t) = U0 * (1-exp (-t / (R * C)))

Stap 2: Die metings

Studente moet die spanning U op tyd t in 'n tabel invoer en dan die eksponensiële funksie teken. As die spanning te vinnig toeneem, moet u die weerstand verhoog R. Aan die ander kant, as die spanning te stadig verander, verlaag R.

As u U0, die weerstand R en die spanning U (t) na 'n sekere tyd t ken, kan die kapasitansie C van die kapasitor hieruit bereken word. Hiervoor moet ons die vergelyking logaritme, en na 'n paar transformasies kry ons: C = -t / (R * ln (1 - U (t) / U0))

Voorbeeld: U0 = 10V, R = 100 kohms, t = 7 sekondes, U (7 sek) = 3,54V. Dan lei C tot 'n waarde van C = 160 μF.

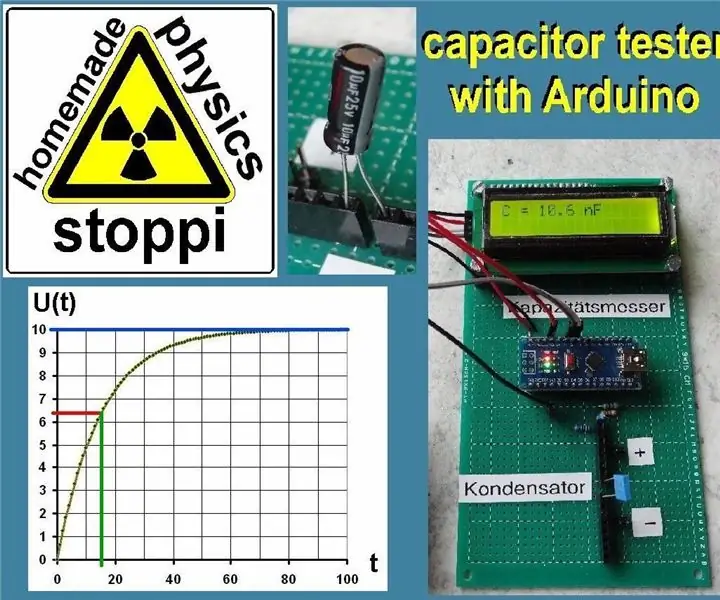
Maar daar is 'n tweede, eenvoudige metode om die kapasiteit te bepaal C. Die spanning U (t) na t = R * C is presies 63,2% van U0.

U (t) = U0 * (1-exp (-R * C / (R * C)) = U0 * (1-exp (-1)) = U0 * 0,632

Wat beteken dit? Studente moet die tyd t bepaal waarna die spanning U (t) presies 63,2% van U0 is. Spesifiek, in die voorbeeld hierbo, word die tyd gesoek waarna die spanning oor die kapasitor 10V * 0,632 = 6,3V is. Dit is die geval na 16 sekondes. Hierdie waarde word nou ingevoeg in die vergelyking t = R * C: 16 = 100000 * C. Dit lewer die resultaat: C = 160 μF.

Stap 3: Die Arduino

Aan die einde van die oefening kan die kapasiteit ook met 'n Arduino bepaal word. Dit bereken die kapasiteit C presies volgens die vorige metode. Dit laai die kapasitor via 'n bekende weerstand R met 5V en bepaal die tyd waarna die spanning by die kapasitor = 5V * 0,632 = 3,16V. Vir die Arduino digitaal-na-analoog-omskakelaar is 5V gelyk aan 1023. Daarom moet u net wag tot die waarde van die analoog-ingang 1023 * 3,16 / 5 = 647 is. Met hierdie tyd kan die kapasiteit C bereken word. Sodat kapasitors met baie verskillende kapasitansie gemeet kan word, word 3 verskillende laaiweerstands gebruik. Eerstens word 'n lae weerstand gebruik om die laaityd tot 647 te bepaal. As dit te kort is, dws as die kapasitansie van die kapasitor te klein is, word die volgende hoër laaiweerstand gekies. As dit ook te klein is, volg 'n 1 Gohms -weerstand aan die einde van die meting. Die waarde vir C word dan op die skerm vertoon met die korrekte eenheid (µF, nF of pF).

Stap 4: Gevolgtrekkings

Wat leer studente in hierdie eenheid? U leer meer oor kapasitors, hul kapasitansie C, eksponensiële funksies, logaritme, persentasieberekeninge en die Arduino. Ek dink baie.

Hierdie eenheid is geskik vir studente tussen 16 en 17 jaar. U het seker al deur die eksponensiële funksie en die logaritme in wiskunde gegaan. Geniet dit in u klas en Eureka!

Ek sal baie bly wees as u vir my in die klaskamerwetenskapkompetisie sou stem. Baie dankie hiervoor!

As u belangstel in my ander fisika -projekte, is my YouTube -kanaal hier:

meer fisika-projekte: