Hoe om 'n geodesiese koepel in Temcor-styl in Autodesk Inventor te skep: 8 stappe

2024 Outeur: John Day | [email protected]. Laas verander: 2024-01-30 07:27

Hierdie handleiding sal u wys hoe u 'n koepel in Temcor-styl kan maak met slegs 'n bietjie wiskunde.

Die meeste inligting in hierdie tutoriaal is verkry uit TaffGoch se omgekeerde ontwerp van die onderverdelingsmetode van die ou Amundsen-Scott Suidpoolstasie, so baie dankie aan hom!

'N Groot voordeel van Temcor -koepels is hul lae unieke stutgetal - dit neem rekenkundig toe met frekwensie, nie anders as Duncan Stuart se gewone triakontahedrale geodetiese rooster (metode 3*), maar die resultaat lyk baie aangenamer.

Vir die eenvoud is die frekwensie van die koepel wat ons maak 14, sodat die akkoordfaktore gekontroleer kan word teen TaffGoch se Temcor-model.

Die Inventor 2016.ipt is aan die einde van die tutoriaal ingesluit.

*OPDATEER*

Ek het Metode 4 beskryf as Duncan Stuart se gereelde triakontahedrale geodetiese rooster, maar dit is nie. Die metode is eintlik uitgevind deur Christopher Kitrick, wat in sy artikel "Geodesic Domes" in 1985 die konstruksie daarvan beskryf het. Boonop skets hy in sy referaat uit 1990, 'A Unified Approach to Class I, II & III Geodesic Domes', 8 ander metodes, waarvan een een is Duncan Stuart se metode 3, die ander sy eie 'Method 4', en, verbasend genoeg genoeg, 'n metode wat soortgelyk is aan Temcor, wat hy 'Metode aa' noem (stap 7 toon hoe Temcor 'Metode aa' verander het). In 'n toekomstige instruksie sal ek die konstruksie beskryf van die metodes wat in laasgenoemde artikel uiteengesit is.

Stap 1: Gebruikersparameters

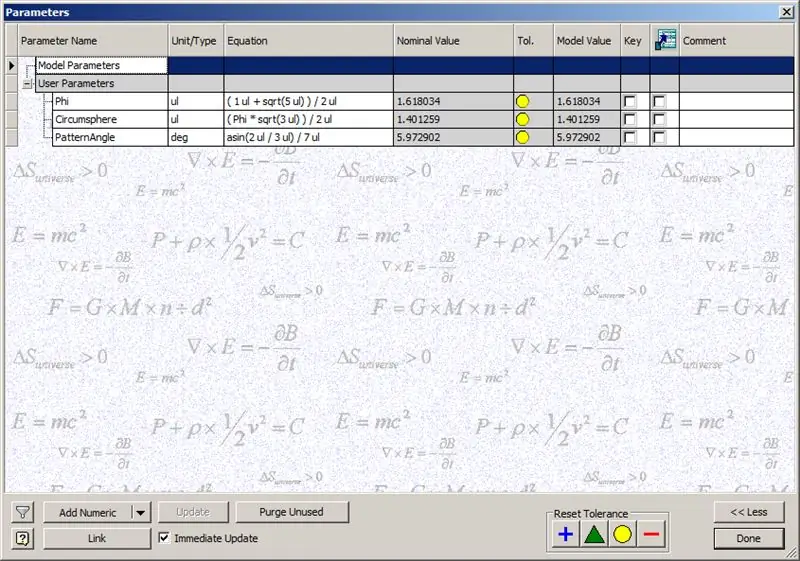
Voer die getoonde parameters in voordat ons begin met die bou van die koepel:

Phi - Die goue verhouding. Omskryf as ((1+√5/) 2

Circumsphere - Dit is die sirkumfeer van 'n dodecahedron, gedefinieer as ((Phi*√3)/2)

PatternAngle - Dit is die sentrale hoek van 'n dodekaëder. Aangesien die frekwensie van ons koepel 14 is, verdeel ons hierdie sentrale hoek met die helfte van die frekwensie, in hierdie geval, 7.

Stap 2: Skets 'n goue reghoek

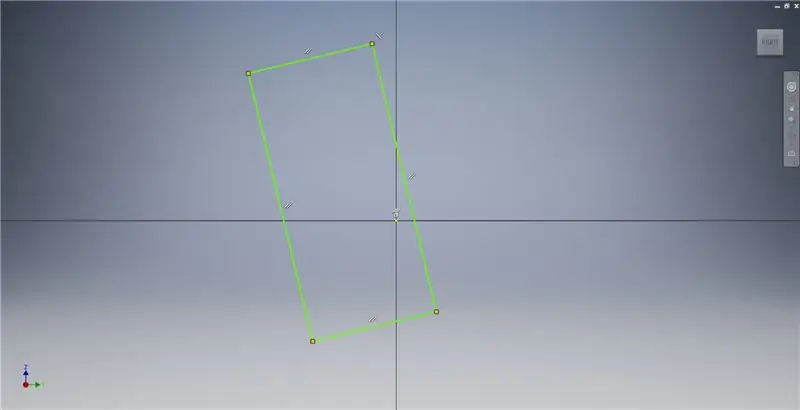
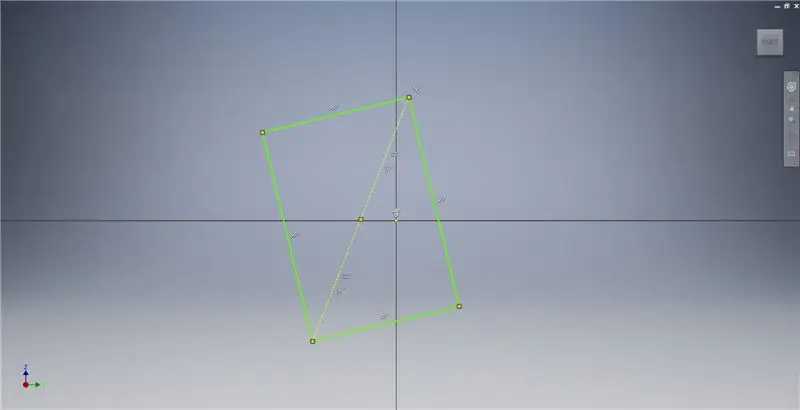
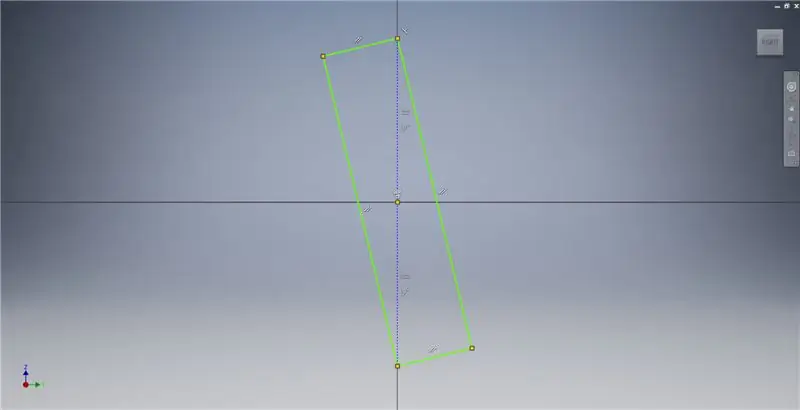
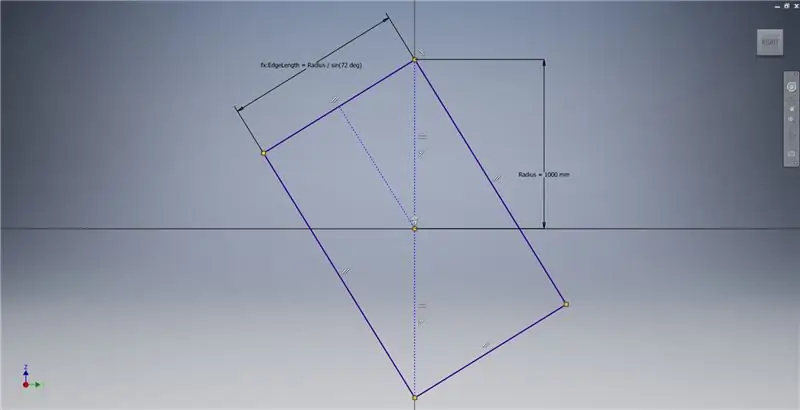
Begin 'n skets op die YZ -vlak, en skep dan 'n driepunt -reghoek soos aangedui, met verwysing na die prentnotas vir meer inligting oor die skepping van 'n goue reghoek.

Stap 3: Maak 'n Golden² -reghoek

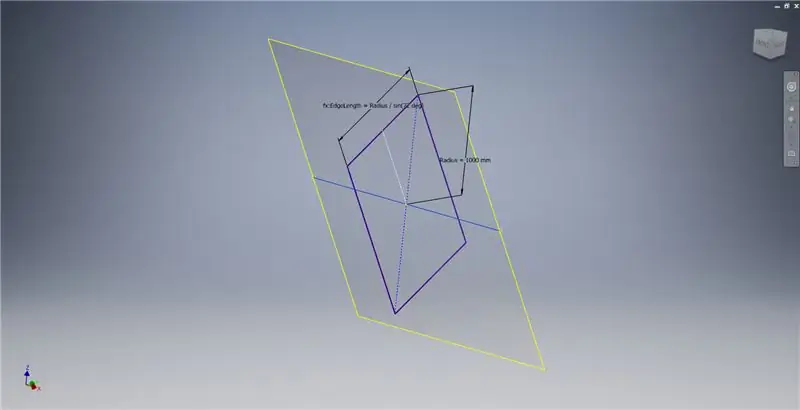
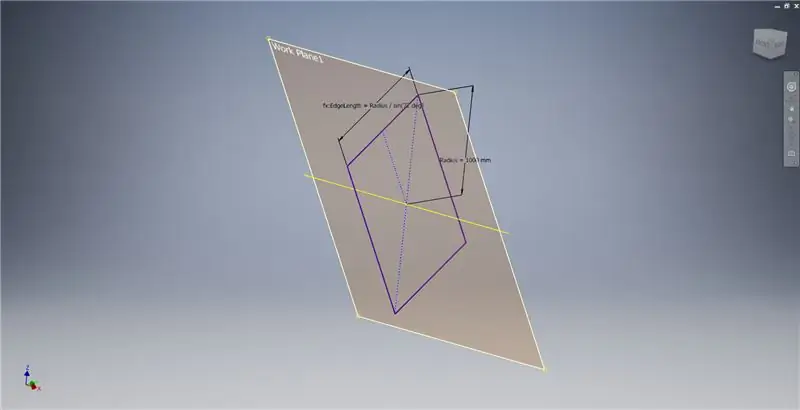
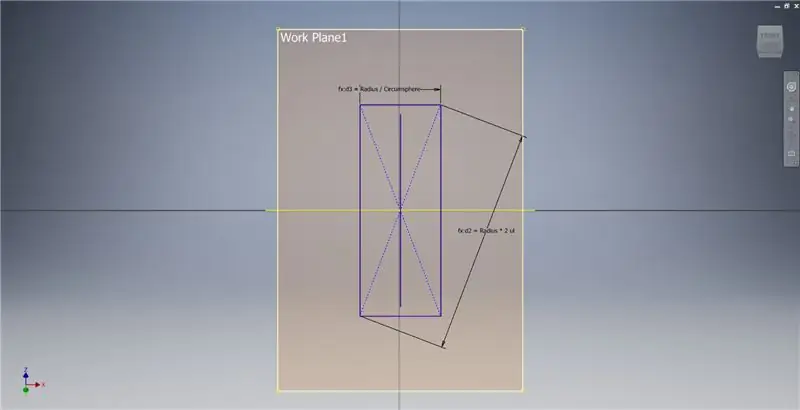
Maak 'n werkvlak met behulp van die X -as en die lyn wat in die eerste prent gemerk is, en begin dan 'n ander skets op hierdie werkvlak. Bou 'n middelpunt -reghoek vanaf die oorsprong, en meet dan die reghoek soos in die derde prentjie getoon.

Stap 4: Maak die 2v Triacon Triangle

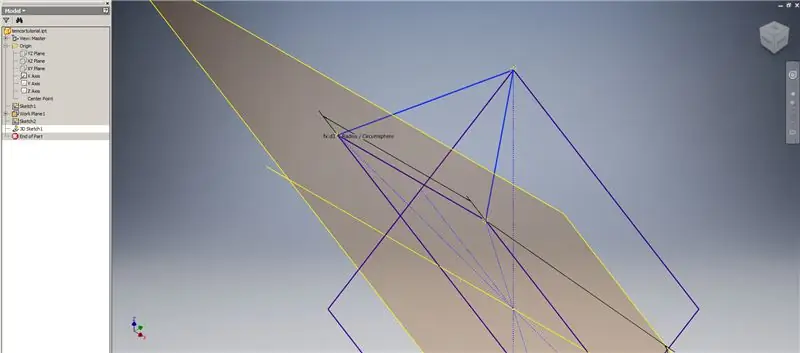
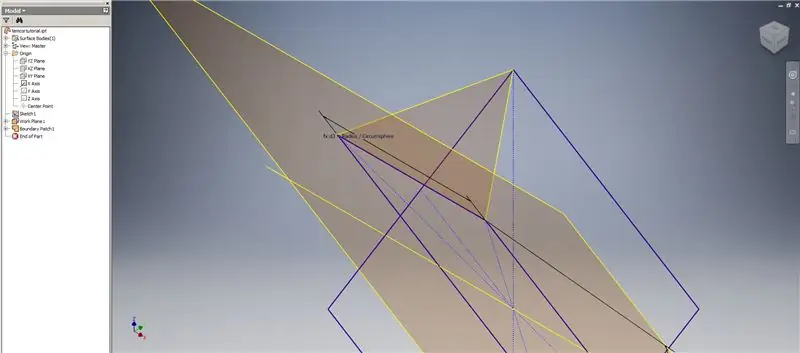
Noudat ons al die meetkunde het wat ons nodig het, vorm u die grensvlek in die tweede prent met die metode wat u verkies. Ek het gekies om 'n 3D -skets te maak, maar skets op 'n ander werkvlak sou net so goed werk.

Stap 5: Skep die kruisingsvliegtuie

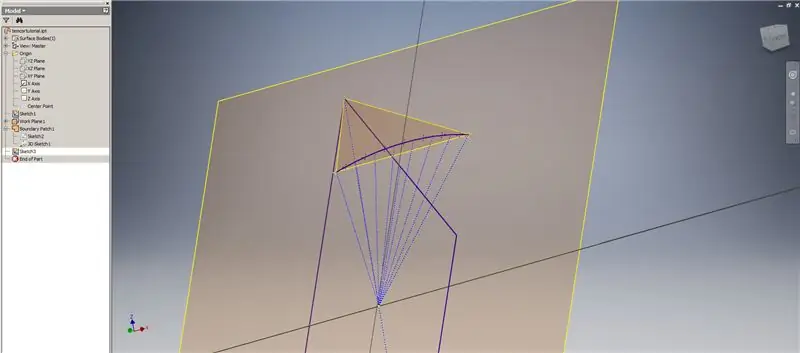
Begin nog 'n skets op die eerste werkvlak ("Werkvlak 1") wat u geskep het, projekteer die hoeke van die Golden² -reghoek, verbind dan hierdie punte en die oorsprong om die sentrale hoek van die 2v triacontahedron te vorm. Deel dit met die helfte van die frekwensie van die koepel, asof u met 'n uiteensetting van metode 2 begin. Plaas punte op die middelpunte van die akkoorde.

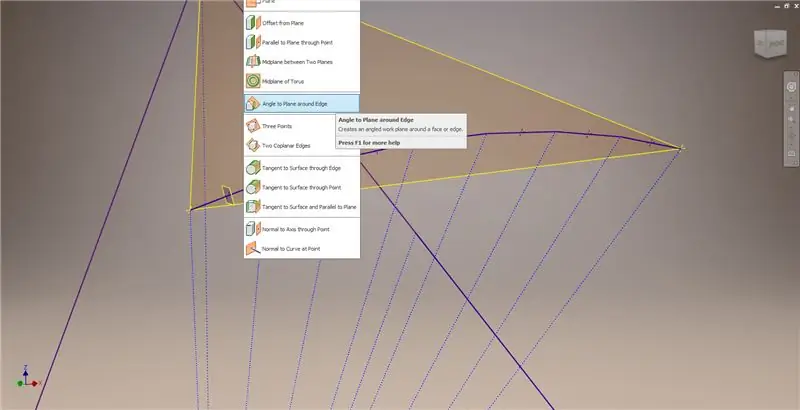
Verlaat die skets en maak dan 'n vlak met behulp van een van die akkoorde en sy middelpunt, soos in die tweede prent getoon. Skep dan 'n ander werkvlak met behulp van 'Angle to Plane around Edge'. Kies Werkvlak 1 en een van die konstruksielyne wat in die middelste regter- en linkeronder -prentjie getoon word. Aanvaar die standaardhoek van 90 grade, anders lyk die res van die onderverdeling nie reg nie. Herhaal die proses met die res van die akkoorde en konstruksielyne om die resultaat in die beeld regs onder te kry.

Stap 6: Skep die kruisingskurwes en vorm die onderverdeling

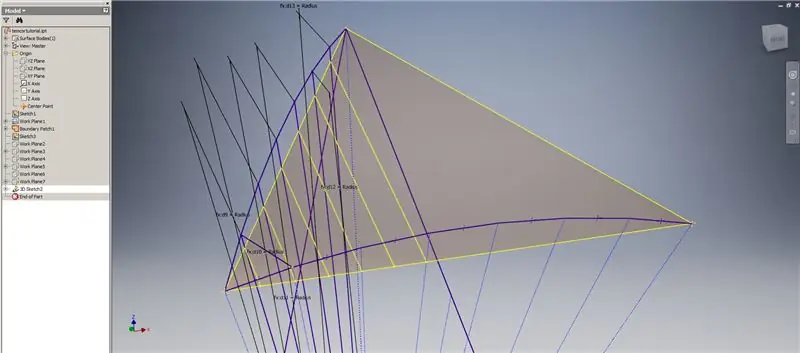
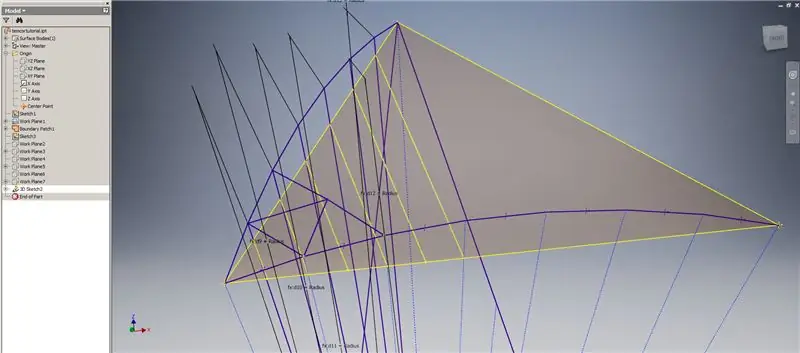
Begin 'n 3D -skets en maak dan kruisingskurwes met behulp van die werkvlakke wat u pas geskep het en die grensvlek, en vorm die lyne in die boonste prent.

Trek lyne wat ooreenstem met die eindpunte van die kruisingskrommes, soos getoon in prent 2. Maak hulle almal gelyk aan die radius van die koepel. Teken die akkoorde wat by die lyne aansluit wat op die kruisingskurwes lê. Verbind enige meetkunde wat naby genoeg lyk om 'n driehoek van die onderverdeling te vorm. Verwys na die volgende 10 beelde waarvoor akkoorde oor die kruisingsvlakvlakke moet weerspieël - dit kan dit beter verduidelik as net woorde.

Stap 7: Voltooiing van die koepel

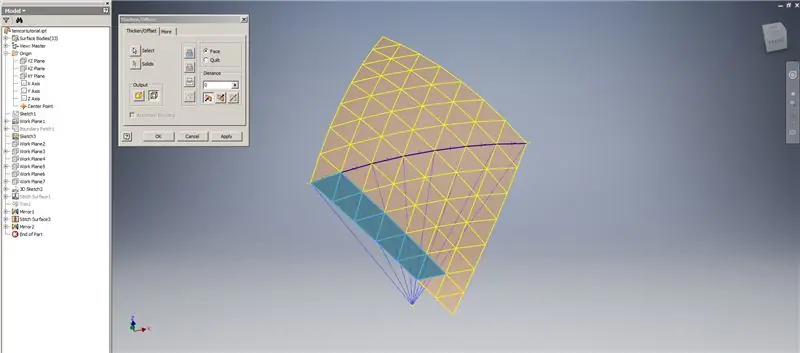
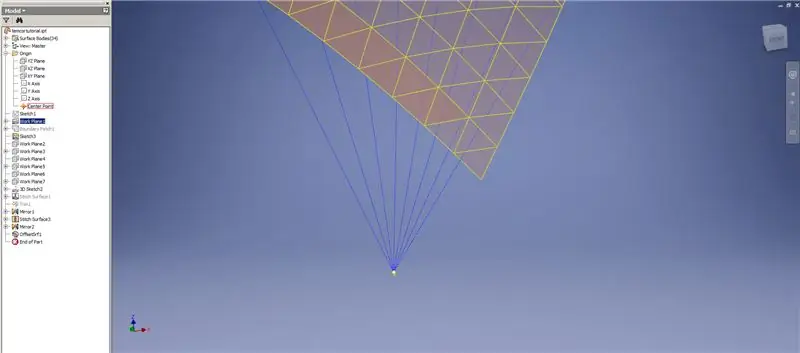
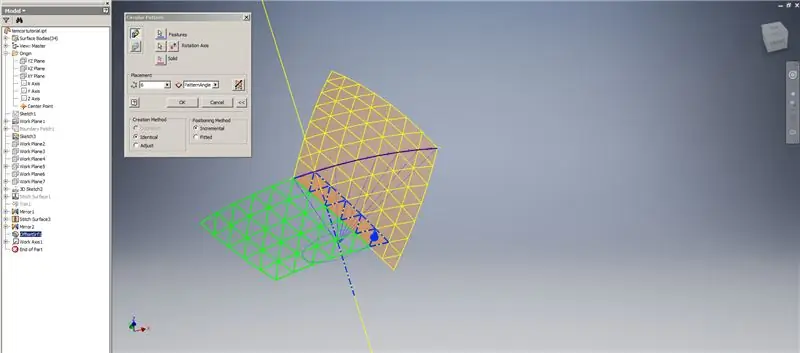
Skep 'n verdikking/verrekening van die onderste rye, en laat die laaste twee rye driehoeke weg. Patroon die nuwe OffsetSrf 6 keer, of ((Frequency = 14)/2) -1. Versteek die OffsetSrf, stik die oppervlaktes met patroon, en weerspieël die gestikte oppervlak met die YZ -vliegtuig. Skep werkvlakke wat op die hoekpunte van die boonste driehoek rus, soos in prentjie 6. Sny die gestikte en spieëlvlakke met hierdie nuwe werkvlakke, en stik dan die oorblywende oppervlaktes saam. Patroon hierdie laaste oppervlak oor die Z -as, steek dan hierdie laaste oppervlaktes saam, en jy is klaar!

Stap 8: Kontroleer akkoorde

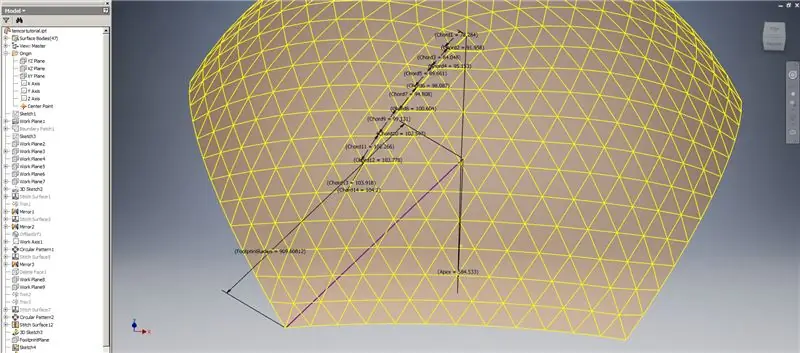
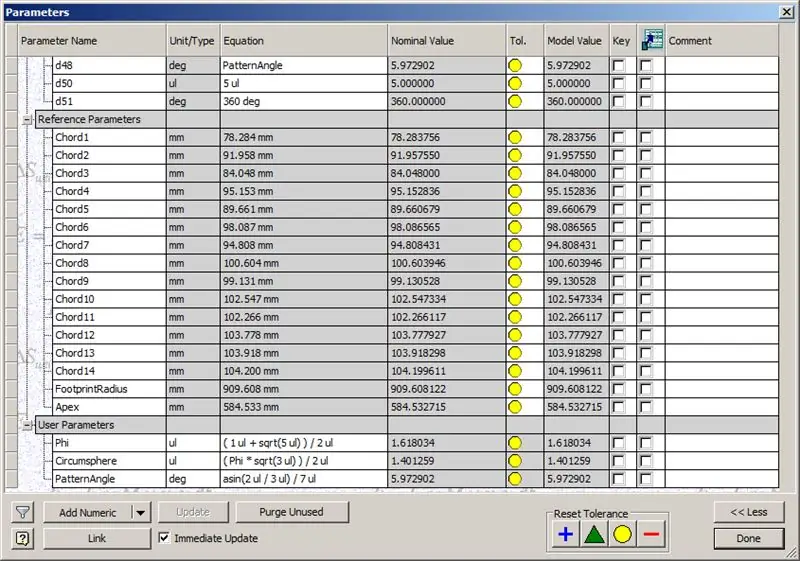
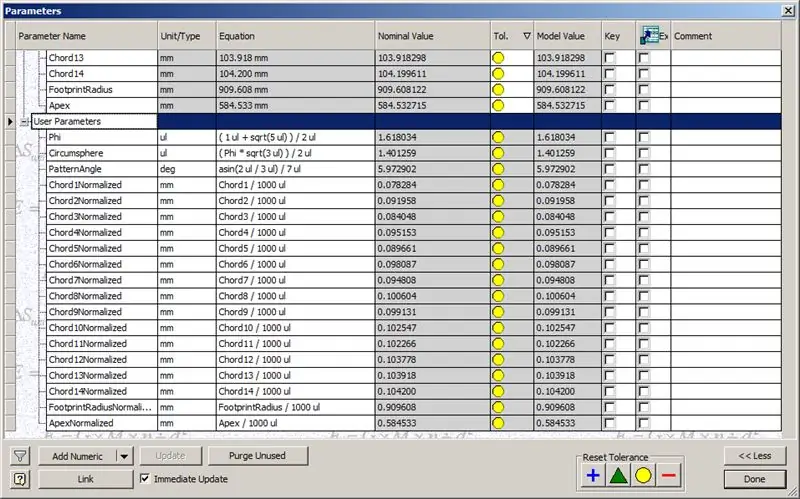
Ons koepel is dus klaar, maar kom ons kyk of die getalle ooreenstem met die model van TaffGoch:

Volgens die verwysingsparameters, lyk dit asof dit 'n perfekte pasmaat is!

Deur die akkoordlengtes met 1000 te deel, kan ons duidelik 'n perfekte ooreenstemming met die akkoordfaktore van TaffGoch se model sien, sowel as die voetspoorradius en toppuntfaktore.