INHOUDSOPGAWE:
- Outeur John Day day@howwhatproduce.com.
- Public 2024-01-30 07:24.
- Laas verander 2025-01-23 12:53.

In hierdie instruksies sal ek verduidelik wat 'n lopende gemiddelde is en waarom u daaroor moet omgee, en u sal wys hoe dit geïmplementeer moet word vir maksimum berekeningseffektiwiteit (moenie bekommerd wees oor kompleksiteit nie, dit is baie eenvoudig om te verstaan en ek sal bied ook 'n maklik gebruikbare biblioteek vir u arduino -projekte:)
Lopende gemiddelde, ook algemeen bekend as bewegende gemiddelde, bewegende gemiddelde of lopende gemiddelde, is 'n term wat gebruik word om die gemiddelde waarde van die laaste N -waardes in datareekse te beskryf. Dit kan net soos die gemiddelde gemiddelde bereken word, of u kan 'n truuk gebruik om 'n minimale impak op die prestasie van u kode te hê.
Stap 1: Gebruikskas: die ADC -metings uitstryk

Arduino het 'n ordentlike 10 bit ADC met baie min geraas. As u die waarde van 'n sensor soos 'n potensiometer, 'n fotoresistor of ander komponente met 'n hoë geraas meet, is dit moeilik om te vertrou dat die meting korrek is.
Een oplossing is om verskeie metings te neem elke keer as u u sensor wil lees en dit gemiddelde. In sommige gevalle is dit 'n lewensvatbare oplossing, maar nie altyd nie. As u ADC 1000 keer per sekonde wil lees, sal u 10 000 moet doen as u gemiddeld 10 metings neem. 'N Groot vermorsing van berekeningstyd.
My voorgestelde oplossing is om 1000 maal per sekonde metings te doen, elke keer die lopende gemiddelde by te werk en dit as huidige waarde te gebruik. Hierdie metode bied 'n mate van vertraging, maar verminder die berekeningskompleksiteit van u aansoek, wat u baie meer tyd gee vir ekstra verwerking.
Op die foto hierbo het ek die gemiddelde gemiddelde van die laaste 32 metings gebruik. U sal sien dat hierdie metode nie 100% foutbestand is nie, maar dat dit die akkuraatheid aansienlik verbeter (dit is nie erger as 'n gemiddelde van 32 monsters elke keer nie). As u elke keer gemiddeld 32 metings wou bereken, sou dit slegs 0,25 ms op Arduino UNO neem vir metings!
Stap 2: Gebruiksgeval: Meet DC -komponent van mikrofoonsein



Arduino kan spanning tussen 0 en Vcc (gewoonlik 5 V) meet. Die klanksignaal is heeltemal AC, en as u dit op 'n mikrobeheerder wil meet, moet u dit ongeveer 1/2 Vcc vooroordeel. In 'n Arduino UNO -projek sou dit ongeveer 2,5 V (DC) + klanksein (AC) beteken. By die gebruik van 10 bit ADC- en 5 V -kragtoevoer, moet die voorspanning van 2,5 V gelyk wees aan die meting van 512. Om 'n AC -waarde van die sein te kry, moet 512 egter van die ADC -meting afgetrek word, en dit is waar?
In 'n ideale wêreld sou dit waar wees. Ongelukkig is die werklike lewe meer ingewikkeld en is ons seinvooroordeel geneig om af te neem. Baie algemeen is 50 Hz -geraas (60 Hz as u in die VSA woon) van die elektriese netwerk. Gewoonlik is dit nie te problematies nie, maar dit is goed om te weet dat dit bestaan. Meer problematies is die lineêre wegdrywing van die verhitting van komponente. U stel die DC -offset -regstelling noukeurig aan die begin in, en dit dryf stadig weg terwyl u toepassing werk.
Ek sal hierdie probleem illustreer met 'n (musiek) maatdetektor. U stel u vooroordeelverwydering op en die slae is duidelik (prent 2). Na 'n geruime tyd beweeg DC -vooroordeel en slae is skaars merkbaar vir die mikrobeheerder (prent 3). Slagopsporingsalgoritme sal in 'n toekomstige instruksie in diepte ondersoek word, aangesien dit die omvang van hierdie artikel oorskry.
Gelukkig is daar 'n manier om voortdurend die DC -verrekening van klank te bereken. Dit sal geen verrassing wees dat die lopende gemiddelde onderwerp van hierdie instruksies 'n oplossing bied nie.
Ons weet dat die gemiddelde waarde van enige wisselsignaal 0. is. Deur hierdie kennis te gebruik, kan ons die gemiddelde waarde van die wisselstroom+GS -sein aftrek, dit is die gelyktydige vooroordeel. Om dit te verwyder, kan ons 'n lopende gemiddelde van die laaste paar waardes neem en dit aftrek van die huidige ADC -lesing. Let daarop dat u 'n lang genoeg loopgemiddelde moet gebruik. Vir klank behoort 'n tiende van 'n sekonde (aantal monsters hang af van u monstertempo) voldoende te wees, maar weet dat langer gemiddeldes beter werk. In die eerste prentjie kan u 'n voorbeeld sien van 'n werklike DC -vooroordeelberekening met 'n lopende gemiddelde met 64 elemente teen 1 kHz monstertempo (minder as wat ek aanbeveel het, maar dit werk steeds).
Stap 3: Berekening

U kan u 'n gemiddelde gemiddelde gewig van mense in die wagkamer van 'n dokter voorstel. Dokter ondersoek een pasiënt en terselfdertyd stap 'n nuwe een die wagkamer binne.
Om die gemiddelde gewig van alle pasiënte wat in die wagkamer wag, uit te vind, kan die verpleegster elke pasiënt vra oor hul gewig, die getalle optel en deel deur die aantal pasiënte. Elke keer as die dokter 'n nuwe pasiënt aanvaar, herhaal die verpleegster die hele proses.
U dink miskien: "Dit klink nie te doeltreffend nie … Daar moet 'n beter manier wees om dit te doen." En jy sou reg wees.
Om hierdie proses te optimaliseer, kan verpleegster 'n rekord hou van die totale gewig van die huidige groep pasiënte. Sodra die dokter 'n nuwe pasiënt ingeroep het, sou die verpleegster hom uitvra oor sy gewig en dit aftrek van die totale groep en hom laat gaan. Verpleegster sou die pasiënt wat pas by die wagkamer ingestap het, vra oor sy gewig en dit by die totaal voeg. Die gemiddelde gewig van pasiënte na elke skof sou die som van gewigte wees, gedeel deur die aantal pasiënte (ja, dieselfde as voorheen, maar nou vra die verpleegster slegs twee mense oor hul gewig in plaas van almal). Ek besef dat hierdie paragraaf 'n bietjie verwarrend kon wees, so kyk na die illustrasie hierbo vir meer duidelikheid (of stel vrae in kommentaar).
Maar selfs al vind u die laaste paragraaf nie verwarrend nie, het u moontlik vrae soos wat aan die begin in die akkumulator moet wees, hoe plaas ek dit wat ek so pas gelees het in 'n werklike C -kode? Dit sal in die volgende stap aangespreek word, waar u ook my bronkode kry.
Stap 4: Die kode

Om die lopende gemiddelde te bereken, moet u eers die laaste N -waardes stoor. U kan 'n skikking met N -elemente hê en die hele inhoud een plek skuif elke keer as u 'n element byvoeg (moenie dit doen nie), of u kan 'n ou element oorskryf en die wyser aanpas na die volgende element om weg te gooi (doen dit asseblief:)
Die akkumulator moet begin met 0, dieselfde geld vir alle elemente in die vertragingslyn. In ander gevalle sal u lopende gemiddelde altyd verkeerd wees. U sal sien dat delayLine_init sorg vir die initialisering van die vertragingslyn; u moet self die akkumulator versorg.
Dit is so maklik om 'n element by die vertragingslyn te voeg, soos om die indeks van die nuutste element met 1 te verminder, om seker te maak dat dit nie die kant van die vertragingsreeksreeks aandui nie. nadat die indeks afgeneem het as dit 0 is, sal dit na 255 loop (omdat dit 'n 8 -bis ongetekende heelgetal is). Modulo (%) operateur met die grootte van die vertragingsreeks, sal verseker dat die indeks na 'n geldige element verwys.
Die berekening van 'n lopende gemiddelde moet maklik verstaanbaar wees as u my analogie in die vorige stap gevolg het. Trek die oudste element van die akkumulator af, voeg die nuutste waarde by die akkumulator, druk die nuutste waarde op die vertragingslyn, gee die opgawe weer gedeel deur die aantal elemente.
Maklik, reg?
Eksperimenteer gerus met die gebruik van die aangehegte kode om beter te verstaan hoe dit alles werk. Soos dit tans lyk, lees arduino analoogwaarde op analoog pin A0 en druk "[ADC waarde], [lopende gemiddelde]" op seriële poort teen 115200 baud rate. As u die seriële plotter van arduino met die regte baud -tempo oopmaak, sien u twee reëls: ADC -waarde (blou) en gladde waarde (rooi).
Stap 5: Ekstras

Daar is 'n paar dinge wat u nie noodwendig hoef te weet om 'n lopende gemiddelde in u projek te gebruik nie.
vertraging: ek begin met die illustrasie van hierdie stap. U sal opmerk dat die lopende gemiddelde van meer elemente 'n groter vertraging inhou. As u reaksietyd vir waardeverandering van kritieke belang is, wil u dalk 'n korter lopende gemiddelde gebruik of die monstertempo verhoog (meet meer gereeld).
Aanbeweeg.
initialisering: Toe ek gepraat het oor die inisialisering van akkumulator en vertragingselemente, het ek gesê dat u hulle almal moet inisialiseer tot 0. Alternatiewelik kan u die vertragingslyn initialiseer na alles wat u wil, maar die akkumulator moet begin as 'n som van die nuutste N -elemente in die vertragingslyn (waar N is die aantal elemente in u lopende gemiddelde). As die akkumulator begin met enige ander waarde, is die berekende gemiddelde verkeerd - te laag of te hoog, altyd met dieselfde hoeveelheid (met dieselfde aanvanklike voorwaardes). Ek stel voor dat u probeer uitvind hoekom dit so is deur 'n pen- en papier -simulasie te gebruik.
akkumulatorgrootte: u moet ook daarop let dat die akkumulator groot genoeg moet wees om die som van alle elemente in die vertragingslyn op te slaan as hulle almal positief of negatief is. Dit beteken feitlik dat die akkumulator 'n datatipe moet wees wat groter is as die vertragingslynelemente en onderteken moet word as die vertragingslynelemente onderteken word.
truuk: lyne met lang vertraging verg baie geheue. Dit kan vinnig 'n probleem word. As u baie geheue beperk is en u nie veel om akkuraatheid steur nie, kan u die gemiddelde gemiddelde benader deur die vertraging heeltemal weg te laat en dit eerder te doen: trek 1/N * akkumulator van die akkumulator af en voeg nuwe waarde toe (op voorbeeld van 8 langlopende gemiddelde: akkumulator = akkumulator * 7/8 + nuwe waarde). Hierdie metode gee 'n verkeerde resultaat, maar dit is 'n goeie manier om die lopende gemiddelde te bereken as u geheue te laag is.
linguistiek: "lopende gemiddelde/gemiddelde" word tipies gebruik wanneer daar na real -time gemiddeldes verwys word, terwyl 'bewegende gemiddelde/gemiddelde' gewoonlik beteken dat algoritme op statiese datastelle werk, soos Excel -sigblad.
Stap 6: Gevolgtrekking
Ek hoop dat hierdie instruksies maklik genoeg was om te verstaan en dat dit u sal help in u toekomstige projekte. Stel gerus vrae in die kommentaar hieronder as daar iets onduidelik is.
Aanbeveel:
Lopende LED met Arduino: 3 stappe

LED met Arduino: dit is lekker om baie beligtings te sien … So ek het gedink of ons LED's met verskillende patrone kan maak? So ek het probeer om dit te maak
Heartcrab: 'n Lambada-lopende robot in jou sak !: 15 stappe (met foto's)

Heartcrab: a Lambada-Walking Robot in Your Pocket !: Dit is een van hierdie projekte met veelvuldige betekenisse: is dit die oulike familielid van die " kopkrappe " van die Half-Life videospeletjies? Miskien 'n lopende robot wat verlief is op 'n lieveheersbeestjie? Of stuur die lieveheersbeestjie haar eie meganisme aan? Wat ook al die antwoord is
CP2 Excel geweegde gemiddelde: 14 stappe
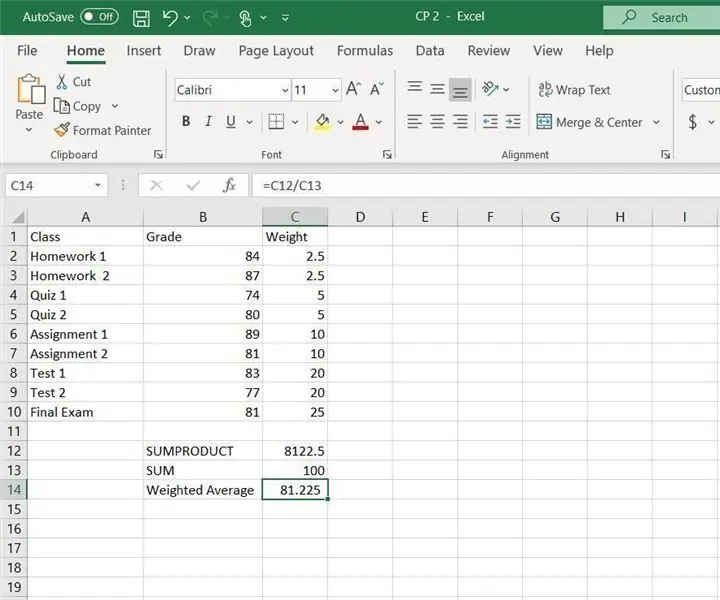
CP2 Excel geweegde gemiddelde: instruksies oor hoe om die geweegde gemiddelde in Excel te bereken. In hierdie voorbeeld sal die SUMPRODUCT en SUM funksie in Excel gebruik word. Die geweegde gemiddelde is nuttig om die algehele graad vir 'n klas te bereken
Bepaal die gemiddelde huidige verbruik van intermitterende toestelle met lae krag: 4 stappe

Bepaal die gemiddelde huidige verbruik van intermitterende toestelle met lae krag: Inleiding Ek wou uit nuuskierigheid weet hoe lank die batterye in my afgeleë temperatuursensor kan hou. Dit neem twee AA -selle in serie, maar dit help min om 'n ammeter in die ry te plaas en na die skerm te kyk omdat die krag verbruik word
Helderder as die gemiddelde beer: 15 stappe

Helderder as die gemiddelde beer: is u helderder as die gemiddelde beer? Hierdie outjie is beslis! Ideaal vir gekke wetenskaplikes, klein Halloween -tonele of mense met 'n verdraaide sin vir humor. (Geïnspireer deur hierdie lamp: http://www.suck.uk.com/product.php?rangeID=104&showBar=1, maar
